Расчет тепловых характеристик водяных воздухоподогревателей

С. А. Лысцев, генеральный директор ЗАО «Антарес ПРО»

В предыдущем номере журнала («Инженерные системы. АВОК СЕВЕРО-ЗАПАД» № 3 2013) была опубликована статья сотрудников НПО «Тепломаш» В. Г. Булыгина и Ю. Н. Марра «О тепловых характеристиках водяных воздухоподогревателей» [1], поставленные в которой вопросы, на мой взгляд, имеют высокую актуальность среди проектировщиков и специалистов по теплоснабжению. Констатируется, в частности, что «часто возникает необходимость пересчитать тепловую мощность при температурах прямой и обратной воды, например, 95 °С/70 °С на температуры 105 °С/70 °С. В этом случае искомой величиной становится расход воды, который будет отличаться от исходного».

В статье много внимания уделено водяным эквивалентам WГ, WХ, W* и анализу их взаимоотношений с коэффициентом эффективности аппарата τ и его производными τх и τ*. Для приведенных в статье выражений для пересчета тепловых параметров требуется рассчитанный с помощью специализированной программы коэффициент эффективности τ. Отмечается, что «расчет при отсутствии программы требует обширных знаний в области теплопередачи и теории теплообменных аппаратов» и производится отсылка читателя к перечню литературы. В статье также имеется упоминание об альтернативной методике расчета тепловых параметров теплообменника с помощью так называемого параметра СК и дается ссылка на статью в журнале «Мир климата» [2], одним из авторов которой я и являюсь. Поэтому постараюсь здесь показать, каким образом для конкретной воздушной завесы на практике можно выполнить упомянутый пересчет тепловых параметров теплообменника при помощи такой характеристики теплообменника, как параметр СК. Эта методика пересчета тепловых параметров теплообменников с помощью параметра СК получила свое развитие именно в последнее время благодаря работам по созданию методики верификации воздушных завес с водяными теплообменниками при Учебно-консультационном центре АПИК, и, скорее всего, в ближайшее время ее  ожидает дальнейшее развитие. Принципы, положенные в основу пересчета тепловых параметров, нашли отражение в статьях сотрудников фирм «Антарес» и «Тропик», участвовавших в разработке методики верификации [2, 3, 4, 5]. Но я бы отметил и весомый вклад в это сотрудников ЗАО НПО «Тепломаш», по крайней мере как принципиальных оппонентов. Прежде всего нужно посчитать значения этого характеризующего работу завесы на максимальной и минимальной скорости параметра СК. В статье [1] в качестве одного из примеров приводится завеса FRICO AD310W. Мы также можем использовать ее для демонстрации пересчета тепловых параметров с помощью параметра СК. В таблице 1 приведены взятые из официального каталога FRICO значения основных тепловых параметров завесы AD310W (тепловая мощность завесы Q, в кВт, и требуемый расход воды через теплообменник G, в л/с) при нескольких наборах эталонных температур (температура воды на входе в теплообменник Tг, температура воды на выходе из теплообменника Tx, температура окружающего воздуха T0) для двух скоростей работы вентилятора завесы (max и min). Так как обычно производители завес предоставляют данные по расходу с меньшей точностью, чем данные по тепловой мощности, то для повышения точности в расчете предпочтительно использовать значения расхода воды (в таблице обозначен как GQ, в л/с), рассчитанные исходя из уравнения теплового баланса:

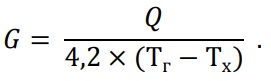
Значение СК «по определению» рассчитывается как произведение расхода воды на отношение разностей температур, воды на входе и выходе теплообменника и воды на выходе теплообменника и температуры окружающего воздуха:

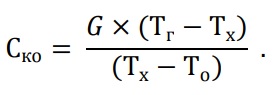
В таблице 1 приведены рассчитанные по формуле (2) значения СК для нескольких наборов эталонных температур и расходов при работе завесы FRICO AD310W на максимальной скорости вентилятора (СК max) и на минимальной скорости (СК min). Те же значения приведены на графике 1 в зависимости от расхода воды в теплообменнике. Видно, что они неплохо аппроксимируются исходя из предложенного в свое время А. В. Пуховым [4] «температурного» подхода выражением:

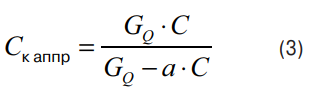
Здесь C и a — используемые при «температурном» подходе константы аппроксимации. При работе завесы FRICO AD310W на максимальной скорости хорошо подходят значения C = 0,098 и a = 0,41. При работе завесы на минимальной скорости подойдут значения C = 0,071 и a =0,45.

Наборы эталонных температур и расходов воды через теплообменник завесы FRICO AD310W и рассчитанные на их основе параметры СК для работы завесы на максимальной и минимальной скоростях вентилятора

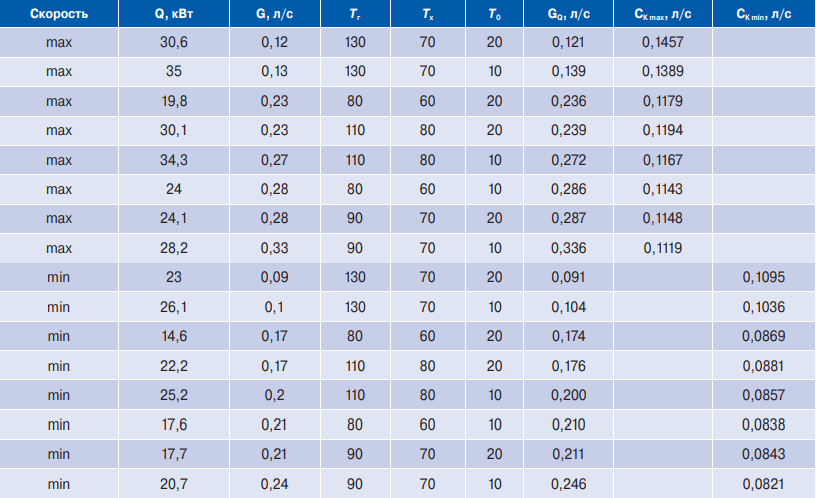
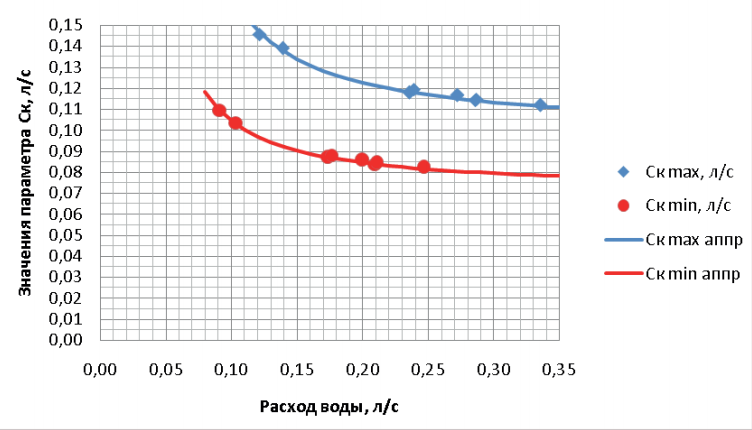
Рис. 1. Зависимость параметра СК для максимальной и минимальной скорости работы вентилятора завесы FRICO AD310W

Параметр СК имеет размерность расхода (л/с) и может выступать в качестве характерной величины, определяющей работу теплообменника при некоторой фиксированной скорости обдува теплообменника. На рис. 1 видно, что при расходах воды, бо льших, чем примерно две величины СК, поведение СК практически перестает зависеть от расхода воды и превращается в константу, которую можно обозначить как СК0. При меньших расходах воды через теплообменник для большинства теплообменников наблюдается рост СК. Однако для некоторых теплообменников при уменьшении расхода воды значение СК не только не растет, но даже может в некотором диапазоне малых расходов снижаться. Происходит это в том случае, если при этих расходах имеет место переход от турбулентного режима движения воды в трубках теплообменника к ламинарному и сопровождающее данный процесс снижение теплопередачи. Физическим смыслом параметра СК является то, что он, согласно его определению (2), численно равен расходу воды через теплообменник, при котором верхняя разность температур (разность температур воды на входе и выходе теплообменника) равна нижней разности температур (разности температуры воды на выходе теплообменника и температуры окружающего воздуха). То есть если значение температуры воды на выходе теплообменника находится посередине между значениями входных температур воды и воздуха, то расход воды через теплообменник G будет равен СК. Для расчета тепловых параметров теплообменника можно использовать два основных подхода. Это «упрощенный подход», предложенный в [2], при котором СК принимается не зависящим от расхода (СК = СК0) и вследствие этого рекомендуемый в случаях, когда рассматриваемые расходы по своей величине больше одной-двух величин СК. А также «температурный» подход [4], способный с хорошей точностью описывать поведение СК вплоть до расходов порядка величины a × C, то есть на практике во всем диапазоне турбулентности водяного потока. Ниже приведены основные формулы для расчета по «упрощенному» и «температурному» подходам (более подробно о них можно посмотреть в статьях [2, 4, 5] либо на сайте www.antar.ru в разделе «Методики и расчеты»).

«Упрощенный» подход.

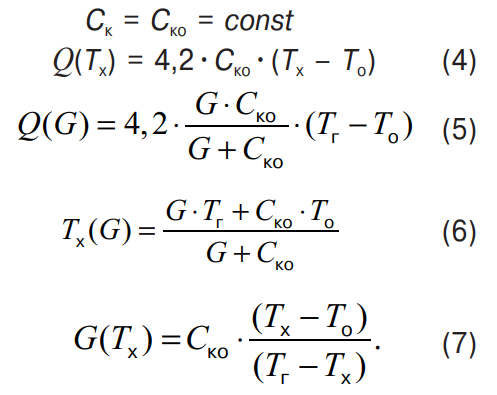
«Температурный» подход.

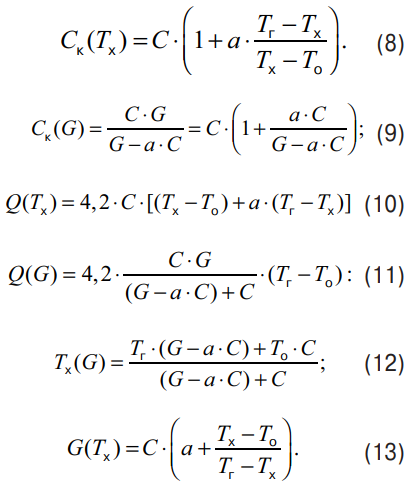
Теперь, зная характерные параметры теплообменника и имея необходимые формулы для пересчета, можно рассчитать, каковы же будут тепловая мощность и расход воды через теплообменник завесы FRICO AD310W при упомянутых выше температурных наборах (95/70/15) и (105/70/15). Используя полученные ранее значения для констант C и a при работе завесы AD310W на максимальной и минимальной скоростях вентилятора, согласно формулам (10) и (13) получаем для максимальной скорости и набора температур (95/70/15):

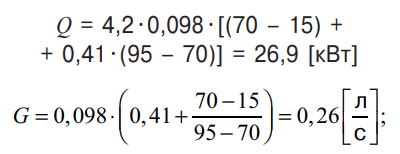
для максимальной скорости и набора температур (105/70/15):

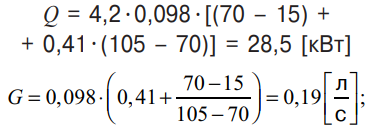
для минимальной скорости и набора температур (95/70/15):

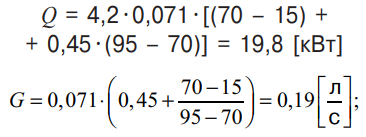
для минимальной скорости и набора температур (105/70/15):

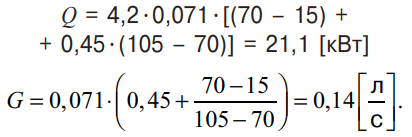
Обратив внимание на формулу (4) «упрощенного» подхода, можно заметить, что в выражении для тепловой мощности нет зависимости от температуры воды на входе в теплообменник. То есть, согласно «упрощенному» подходу, не важно, какова температура воды на входе в теплообменник. Тепловая мощность теплообменника преимущественно определяется характеризующим его параметром СК0 и разностью температур воды на выходе теплообменника и окружающего воздуха. Так, подставив в (4) принятые в качестве СК0 средние от представленных в таблице значений для максимальной скорости СК0 = <СК max> = 0,12 и для минимальной скорости СК0 = <СК min> = 0,09, получим примерно те же значения тепловой мощности, что были полученыранее с использованием формул «температурного» подхода:

для максимальной скорости:

для минимальной скорости:

Литература
1. В. Г. Булыгин, Ю. Н. Марр. О тепловых характеристиках водяных воздухоподогревателей — Инженерные
системы АВОК Северо-Запад, № 3.
2013.
2. С. А. Лысцев, А.В. Азин. Методика оценочного расчета тепловых параметров водяных завес — Мир климата, № 76. 2013.
3. С. А. Лысцев, А. В. Азин. Методика оценочного расчета тепловых параметров применительно к радиаторам
водяного отопления — Мир климата,
№ 77. 2013.
4. А. В. Пухов. Мощность тепловой завесы с жидким теплоносителем в общем
случае — Мир климата, № 78. 2013.
5. А. В. Пухов. Мощность тепловой завесы при произвольных расходах теплоносителя и воздуха — Мир климата, № 80. 2013.

Комментарий специалиста

А. В. Пухов, технический директор компании «ТРОПИК»

Рассматриваемая статья имеет отношение к расчету тепловой мощности воздушных завес или, правильнее будет сказать, к пересчету этой мощности, приведенной для некоторых условий работы воздушной завесы, к другим условиям. Закономерности этого пересчета обсуждались, в том числе, и в моих работах [4] и [5]. Различие в обозначениях физических величин в статье и вышеуказанных работах заключается в несовпадении символа для тепловой мощности завесы, которая здесь приводится как Q, а у меня как W. В этом комментарии я также буду использовать для обозначения мощности принятое автором обозначение Q. В статье приводится большое число формул для пересчета мощности и других характеристик тепловых завес, и некоторые из этих формул могут показаться достаточно сложными. Поэтому, прежде всего, я хотел бы показать, что все эти соотношения являются следствиями очень простых физических закономерностей. Для простоты я не буду учитывать и размерный коэффициент 4,2 кДж/кгК.
Итак, рассмотрим работающую при температуре воздушного окружения Т0 воздушную завесу. Проходящий через теплообменник завесы воздух этой температуры, нагреваясь, охлаждает поступающую в теплообменник горячую воду от значения температуры Тг до значения Тх на выходе из теплообменника. Теория теплообмена подразумевает для мощности теплообмена в случае, если основную роль в передаче тепла играет теплопроводность (и, возможно, вынужденная конвекция), пропорциональность мощности теплообмена некоторой эффективной разности температур обменивающихся теплом сред. То есть, в самом общем виде: Q = KΔТэфф, где К — некоторый интегральный коэффициент, зависящий от теплопроводности материалов и сред, геометрии (в том числе, толщины и площади) теплообменника, интенсивности конвекции и т. д., а ΔТэфф — также некоторая усредненная по всей площади теплообмена разность температур сред, которые участвуют в теплообмене. Можно предположить, что при фиксированной скорости воздушного потока значения К будут постоянны для широких интервалов температур воды и воздуха. Эффективная разность температур обмена — очевидно, разность между некоторой, неизвестной заранее, «средней» температурой воды ТW в теплообменнике и температурой воздуха Т0. На этом вся несложная физика теплопередачи заканчивается. Далее уже из обработки опытных данных множества производителей воздушных завес оказалось [2], что в первом приближении можно считать, что ТW = Тх, то есть средняя температура воды, которая участвует в обмене, — это именно температура холодной воды. Для этого приближения указанная выше формула для мощности принимает вид Q = Cк(Тх – Т0), где Ск — это принятое для этого случая обозначение коэффициента К автором в работе [2]. И практика показывает, что при достаточно большом расходе воды G через теплообменник коэффициент Ск практически постоянен, что и оправдывает применение этого метода для расчета тепловой мощности. Здесь требуется пояснить, что же такое большой или малый расходы воды в терминах температур Тг, Тх и Т0? Если расход большой, то вода, проходя через теплообменник, не успевает заметно охладиться, и значение Тх будет близко к значению Тг. Если же расход очень мал, то вода охладится почти до значения температуры окружающего воздуха Т0. Таким образом, если Тг – Тх < Тх – Т0, можно сказать, что расход воды большой, а если Тг – Тх > Тх – Т0, то малый (область же средних расходов этого значения Тг – Тх ≈ Тх – Т0).
Tеперь, чтобы применить метод пересчета мощности, обозначенный автором как упрощенный подход, необходимо подсчитать из соотношения Q = Cк(Тх – Т0), используя данные мощности, приведенные производителем для некоторых условий, коэффициент Ск. Таким образом, лишь одно значение мощности при некоторых условиях Тг, Тх, и Т0 позволяет производить пересчет к другим значениям расхода воды и температур. Это и есть сущность упрощенного подхода к пересчету.
Ограничением упрощенного подхода можно считать пренебрежение учетом влияния температуры воды Тг, поступающей в теплообменник. Даже если эта степень влияния очень мала, требуется указать ее количественное выражение. Это позволит, во-первых, определить границы применимости упрощенного подхода, а во-вторых, производить более точные расчеты в тех случаях, когда упрощенный подход приводит к неприемлемым погрешностям. 

Эти рассмотрения были проведены мной в работах [4] и [5]. Для учета влияния температуры горячей воды средняя температура участвующей в теплообмене воды ТW была принята равной не Тх, а Тх + αΔТW, где ΔТW = Тг – Тх — это изменение температуры воды, проходящей через теплообменник, и α — некоторая постоянная, которая, скорее всего, заметно меньше единицы. По аналогии с Ск константу пропорциональности для мощности теплообмена для этого случая я обозначил С. Этот подход именуется автором в своей работе температурным. В отличие от упрощенного подхода наряду с коэффициентом общей мощности теплообмена (Ск или С), характеризующим воздушную завесу, в нем также явно учитывается степень влияния на теплопередачу горячей воды (это и есть α). Пренебрежение этой степенью влияния математически равноценно приближению α = 0, а по физическому смыслу эквивалентно рассмотрению, принятому в упрощенном подходе. В общем случае с учетом влияния на теплообмен горячей воды для мощности теплопередачи получим: Q = C(Тх – Т0 + αΔТW). Это основное, найденное мной уравнение, которое позволяет выражать мощность воздушной завесы до существенно более низких расходов, чем упрощенный подход. Для нахождения констант С и α потребуется уже два значения мощности воздушной завесы. Ко времени написания работы [4] я исследовал несколько воздушных завес, и коэффициенты α при максимальном воздушном потоке для всех из них укладывались в область значений 0,1÷0,14. По этой причине я принял его неким средним значением α = 0,12, хотя и оговорил возможность принятия коэффициентом α других значений. При написании работы [5] мной были обработаны данные для большого количества завес, а также программы производителей теплообменников для воздушных завес. Для некоторых завес значения коэффициента α были существенно больше, указанных выше, но и они подтверждали преимущественное влияние температуры Тх на теплообмен. Это в моем представлении оправдывает предложенный автором принцип упрощенного подхода.
Существенное отличие между упрощенным и температурным подходами заключается в том, что для полного описания тепловых характеристик в рамках упрощенного подхода требуется значение мощности завесы лишь в одной точке рабочих параметров, в то время как при более точном температурном подходе — в двух. Эти точки следует выбирать так, чтобы одна из них относилась к области больших расходов, а другая, по возможности, к области средних, хотя при достаточно точных данных мощностей обе точки могут быть выбраны в рабочей области параметров произвольно. Распределение значений α для различных воздушных завес и программ производителей теплообменников, которые были исследованы мной, выглядит следующим образом: самые малые встречающиеся значения α при максимальной скорости воздушного потока — 0,085, большая доля воздушных завес имеет α в области значений 0,1÷0,25, и значительно реже воздушные завесы имеют значения α большей величины. Следует заметить, что возможно скомбинировать преимущества и упрощенного и температурного подходов, чтобы посредством единственного достаточно точного измерения тепловых свойств завесы получить максимум информации о ее характеристиках при любых условиях. И хотя единственное измерение математически не позволит вычислить две константы для любой исследуемой завесы, одну из них можно назначить произвольно. Пусть имеется некоторая воздушная завеса, о которой мы предположительно не знаем ничего, кроме единственного значения мощности при некоторых условияхее работы.

Однако мы можем предположить, что ей соответствует некоторый коэффициент α0 степени влияния температуры горячей воды на теплообмен и что его значение больше чем 0,085. Если приписать этому коэффициенту α = 0,15, то можно видеть, что оно всегда будет располагаться ближе к реальному неизвестному α0, чем α = 0, что является точным выражением применяемого сейчас упрощенного подхода. Хотя прямое вычисление α по двум рабочим точкам всегда даст большую точность пересчета мощности. Эффективная температура воды в этом приближении: ТW = 0,85Тх + 0,15Тг, и для мощности будет справедливо выражение: Q = C(0,85Тх + 0,15Тг – Т0) для любых значений указанных температур. Если для некоторых фиксированных значений температур (например, для Тх = 70 °C, Тг = 95 °C и Т0 = 15 0С или, в более удобных обозначениях, 95/70 при 15) мощность воздушной завесы принимает значение Q0, то, применяя вышеуказанное уравнение для мощности, получим: С = Q0/58,75 °C и, окончательно, Q = Q0(0,85Тх + 0,15Тг – То)/59 °C. Эта формула с достаточной точностью позволяет вычислять мощность завесы для случаев больших, средних и малых водяных расходов (или, другими словами, в широких областях изменения Тг, Тх и Т0). Она пригодна для широкого спектра практических задач использования воздушных завес. Если значение Q0 задано для другого набора температур, например, 80/60 при 20, то, повторяя все несложные приведенные выше рассуждения, которые читатель сможет сделать сам, получим для мощности: Q = Q0(0,85Тх + 0,15Тг – То)/43 0С. Хотелось бы подробнее остановиться и на физическом смысле малости степени влияния на мощность теплообмена значения температуры горячей воды (или малости α), что является основным предположением в [2]. Температура воды в теплообменнике воздушной завесы изменяется от значений Тг до значений Тх. Однако это падение температуры не происходит постоянно с одинаковой
скоростью. Быстрое начальное изменение температуры любой из сред при теплообмене сменяется плавным по мере приближения сред к температурному равновесию. Это является следствием пропорциональности мощности обмена разностям температур сред и приводит к тому, что средняя температура воды в теплообменнике будет существенно ниже, чем (Тг + Тх)/2.

Ю. Н. Марр, главный конструктор
ЗАО «НПО «Тепломаш»

В статье С. А. Лысцева предлагается рассчитывать тепловые характеристики водяных воздухонагревателей на произвольные по температурам и расходу греющего теплоносителя условия, используя приведенные производителем каталожные данные. Для пересчета применяется предложенный автором так называемый альтернативный метод, опирающийся на коэффициент Ск (некий условный расход греющего теплоносителя). В нашей статье, на которую автор ссылается, проведено подробное исследование этого метода и показано, что никакой он не альтернативный, а плоть от плоти теории теплообменных аппаратов. Единственная его особенность в том, что коэффициент Ск нащупан эмпирическим путем как некий инвариант без знания основ теории теплообменных аппаратов. Вместо Ск мы ввели его безразмерный аналог τ* и установили связь [равенство (6)] с коэффициентом эффективности теплообменного аппарата τ — основным параметром теории, являющимся решением дифференциального уравнения теплопередачи в теплообменнике. Там же было показано, в каких границах можно считать τ* с некоторой точностью инвариантом, а где шансов на это нет. Предлагая, на первый взгляд, привлекательную возможность воспользоваться уже имеющимися каталожными данными, С. А. Лысцев почему-то не принял во внимание ни один из результатов нашего исследования. Как выяснилось, параметр τ* (а значит, и Ск) очень чувствителен к начальной температуре горячей воды, во много раз более чувствителен, чем τ. При отношении водяных эквивалентов Wг/Wх ≤ 1 (горячего теплоносителя к холодному) в диапазоне температур воды 60– 130 °C ошибка в τ не превосходит 18%, тогда как ошибка в τ* достигает 200%. При Wг/Wх ≥ 1 ошибка в том же температурном диапазоне может достигать 14% для низких нагрузок по расходу воздуха и убывает с увеличением нагрузки.

В. Г. Булыгин, генеральный директор
ЗАО НПО «Тепломаш»

Тепловые характеристики в каталогах обычно приводятся по одной на каждую стандартную температуру горячей воды. Поэтому то обстоятельство, что расположение расчетных точек (Ск от расхода воды) на графике в статье С. А. Лысцева допускает обобщение всего массива одной кривой или аппроксимацию одним уравнением, не может служить безоговорочным основанием возможности пересчета тепловых характеристик. На самом деле через массив каталожных точек пройдет столько кривых, сколько нанесено точек. При этом массив значений Ск (или, что то же, τ*) будет иметь значительно большее расхождение, чем если бы С. А. Лысцев воспользовался величинами τ. И ошибка при пересчете по Ск также может оказаться больше, чем по τ. Предлагаемый автором пересчет характеристик возможен, во-первых, при небольших отклонениях температуры воды от каталожной (приблизительно 10–15 °C), и, во-вторых, для надежности следует ограничить диапазон применимости не размерным расходом воды, а строгим неравенством Wг/Wх ≥ 1. Помимо отмеченного статья перегружена демонстрацией владения арифметическими действиями, что, понятно, не имеет научного интереса. Зато непонятно, зачем приведен рис. 2, о котором в статье нет речи.