Ослабление струи воздушной завесы. Сравнение аппроксимирующих функций

В прошлом номере журнала «МИР КЛИМАТА» была опубликована статья «Ослабление струи воздушной завесы (по результатам верификации)», основными целями которой были рассмотрение и предварительный анализ результатов проведенной за последнее время в УКЦ АПИК верификации воздушных завес, а также выявление закономерностей, присущих прошедшим верификацию завесам. В качестве дополнительного вопроса рассматривалась приемлемость предложенного сотрудниками НПО «Тепломаш» выражения для значения максимальной скорости воздуха на оси струи завесы. То есть, имелось желание проверить, насколько согласуются полученные в результате верификации данные замеров максимальной скорости на оси струи с предлагаемым в стандарт по воздушным завесам выражением:

где ϑ_m— максимальная скорость на оси основного участка стандартной турбулентной струи, ϑ₃ — средняя скорость истечения струи из сопла, b₃ — ширина сопла, x — расстояние от сопла вдоль оси струи. В том же номере журнала Ю. Н. Марр в отзыве на упомянутую статью отметил, что, по крайней мере, для воздушной завесы КЭВ-6П201Е данные верификации противоречат предлагаемой формуле. Постараемся здесь показать, что причиной указанного противоречия могут являться не только и не столько ошибки и неточности в проведении измерений, сколько некорректности, имеющие место в самой формуле (1). При этом более подробно остановимся на представленной в предыдущей статье формуле распространения аффинной воздушной струи, а также на том, в чем ее сходство и различие с формулой (1).

В своем рассмотрении будем исходить из нескольких допущений. Во-первых, будем рассматривать здесь только плоскопараллельные струи, не ограниченные по краям. Во-вторых, будем исходить из постоянства полного количества движения секундной массы воздуха в сечениях плоскопараллельной струи, то есть сохранения количества движения вдоль струи. В-третьих, расширение воздушной струи по мере продвижения вдоль оси будем считать линейным. Хотя недавние результаты программного моделирования распространения струи, проведенного А. В. Пуховым (компания «Тропик»), на мой взгляд могут свидетельствовать о нелинейном характере расширения плоскопараллельной воздушной струи. Наконец, в-четвертых, допустим, что любой профиль скоростей в начальном сечении струи по мере продвижения вдоль оси струи преобразуется в аффинный. При этом скорость воздуха в каком-либо сечении преобразованной струи дается выражением:

где f(y) — некоторая функция, определяющая аффинный профиль скоростей в сечении струи.

Начальные профили скоростей в сечении струи воздушной завесы обычно имеют сложную форму и уникальны для каждой завесы. Для примера на рис. 1 и 2 представлены продольные и поперечные профили скоростей завесы «Антарес» модель 1202ESd серии «Универсал ПРО», полученные по результатам верификации в УКЦ АПИК.

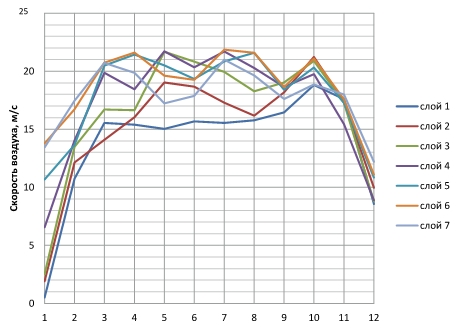
Рис. 1. Продольные профили скоростей в начальном сечении воздушной струи завесы «Антарес» модель 1202ESd по результатам верификации

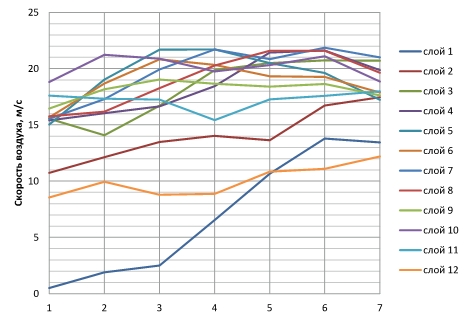
Рис. 2. Поперечные профили скоростей в начальном сечении воздушной струи завесы «Антарес» модель 1202ESd по результатам верификации

По мере продвижения вдоль струи происходит расширение струи и сглаживание профилей скоростей. На рис. 3 показано смоделированное преобразование начального П-образного профиля скоростей в сечении плоскопараллельной воздушной струи по мере продвижения вдоль оси струи (здесь L — относительное расстояние от начала струи).

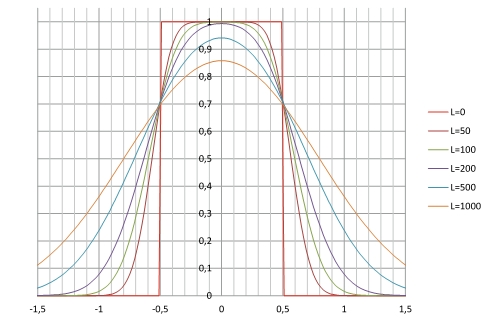
Рис. 3. Преобразование П-образного профиля скоростей воздуха в аффинный профиль скоростей в сечении воздушной струи по мере продвижения вдоль оси струи

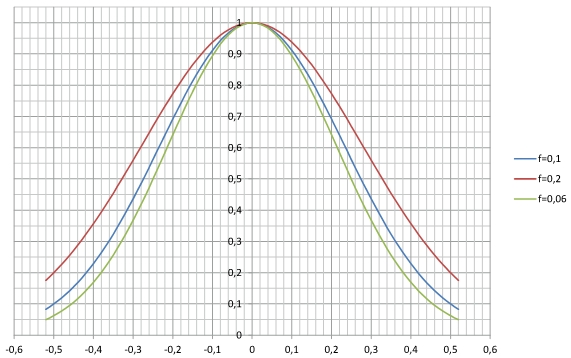
Рис. 4. Аффинные профили скоростей в сечении струи в зависимости от критерия определения границ струи

На начальном этапе происходит «размытие» боков струи (кривая «L=50»), вплоть до соединения размытия обоих краев струи (кривая «L=200»). До этого этапа максимальная скорость на оси струи остается неизменной. Последующее расширение струи сопровождается уменьшением максимальной скорости на оси струи. При этом произведение среднего от квадрата скорости на толщину струи в сечениях струи, а значит, и количество движения секундной массы воздуха струи остаются неизменными.

В качестве одного из вариантов аппроксимации профиля скоростей в сечении плоской воздушной струи, к которому преобразуется любой начальный профиль, предложено использовать функцию нормального распределения, приведенную в работе Г. Н. Абрамовича «Теория турбулентных струй»:

где b — толщина струи в рассматриваемом сечении струи. Характерным свойством нормального распределения является его аффинность, неизменность при масштабировании. Профили скоростей в сечениях сформировавшейся плоскопараллельной струи переходят один в другой растяжением или сжатием вдоль осей абсцисс и ординат.

Значение коэффициента β в формуле (3) зависит от того, на основании какого критерия определяются границы профиля струи. Так, если в качестве граничных пределов струи выбираются точки y=±b/2, значения аппроксимационной функции в которых составляют 0,1 от максимального, то значение коэффициента β = 9,2. Если принимается f (±b/2) = 0,2, то β=6,4. Если же толщина струи определяется таким образом, чтобы аппроксимационная функция имела половинные значения от максимального на расстояниях от оси струи y=±b/4, то коэффициент β в аппроксимационной функции будет равен 11,1. При этом на краях струи будет значение f = 0,06. На рис. 4 представлены графики аппроксимационных аффинных функций для перечисленных условий.

Стремление формы профиля скоростей в сечении струи воздуха к форме нормального распределения (3) по мере продвижения вдоль оси струи можно пояснить следующим образом: объем струи условно разделим на небольшие объемные элементы, которые движутся со скоростью, значение которой зависит от местонахождения элемента внутри струи. При движении внутри струи завесы компактные объемные элементы воздуха взаимодействуют друг с другом, что сопровождается перераспределением их количеств движения (импульсов) по аналогии с перераспределением импульсов шаров доски Гальтона. Такие хаотичные столкновения большого количества компактных объемных элементов приводят по мере продвижения вдоль оси струи как к расширению струи вследствие появления поперечных составляющих импульса, так и к формированию распределения импульса в сечении струи в виде нормального Гауссова распределения. Так как количество движения секундной массы воздуха пропорционально квадрату скорости воздуха, а любая степень от нормального распределения также имеет форму нормального распределения, то и профиль скоростей воздуха в сечении струи по мере продвижения вдоль оси струи стремится приобрести форму нормального распределения.

Для аффинного профиля скоростей как средняя скорость, так и среднее от квадрата скорости пропорциональны максимальной скорости в сечении струи и не зависят от значения толщины струи. Значение средней скорости <ϑ> (в формуле (1) средняя скорость в сечении на выходе из сопла обозначена как ϑ₃) в рассматриваемом произвольном сечении аффинной струи можно оценить с помощью интеграла Гаусса:

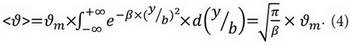
Среднее значение квадрата скорости <ϑ²>в сечении аффинной струи находится аналогичным образом:

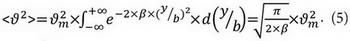
Таким образом, для профиля скоростей в сечении аффинной струи с функцией нормального распределения квадрат средней скорости и среднее от квадрата скорости пропорциональны квадрату максимальной скорости воздуха в сечении и зависят от критерия выбора границ струи. При значении β=11,1 значение квадрата средней скорости в сечении струи —

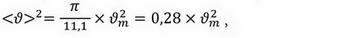
а значение среднего от квадрата скорости —

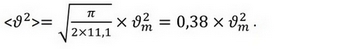
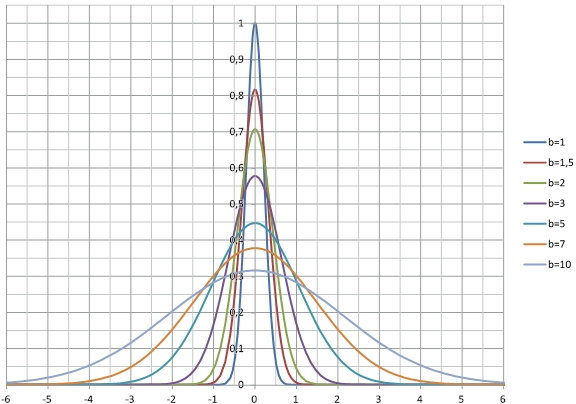
Рис. 5. Эволюция профиля скоростей воздуха в сечении аффинной струи по мере продвижения вдоль оси струи

Но это в том случае, когда интегрирование ведется по бесконечным пределам. Если же интегрирование проводится по толщине струи, то коэффициенты пропорциональности значению ϑ²_m для <ϑ²>и <ϑ>² окажутся несколько меньше, опять же в зависимости от принятого критерия определения толщины струи.

В отзыве Ю. Н. Марра, опубликованном в прошлом номере журнала, говорится, что в «Справочнике по гидравлическим сопротивлениям» И. Е. Идельчика приводится пропорциональность среднего от квадрата скорости квадрату максимальной скорости с коэффициентом 0,49. В таком случае, исходя из (5), значение β=6,5. Это означает, что в качестве граничных принимаются условия, при которых значение скорости на краях профиля скоростей составляет 1/5 от максимальной скорости в сечении струи.

Количество движения секундной массы воздуха через некоторое малое сечение есть произведение секундной массы воздуха (расхода) через это малое сечение на скорость этой секундной массы. А так как расход сам пропорционален скорости воздуха, то количество движения секундной массы воздуха оказывается пропорционально квадрату скорости воздуха, проходящего через рассматриваемое малое сечение. Полное количество движения секундной массы воздуха в сечении струи пропорционально произведению среднего от квадрата скорости воздуха в сечении струи <ϑ²> на толщину струи в рассматриваемом сечении вне зависимости от формы профиля скоростей в сечении струи. Из принятого допущения о постоянстве количества движения секундной массы воздуха на всем рассматриваемом протяжении струи следует, что произведение среднего от квадрата скорости воздуха на толщину струи в любом сечении струи должно быть постоянным:

Для аффинной струи при условии принятых допущений о постоянстве полного количества движения секундной массы воздуха и о линейном расширении струи с коэффициентом пропорциональности α можно записать:

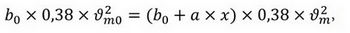
где ϑ_m0 — максимальная скорость в начале струи, b₀ — начальная толщина струи, x — расстояние между рассматриваемыми сечениями. Тогда для максимальной скорости на оси аффинной плоскопараллельной струи получаем выражение:

Значение параметра расширения струи также зависит от выбора критерия определения толщины струи. Так, если критерием выбора границ струи является условие f(±b/2)=0,06, то коэффициент пропорциональности будет больше на 32 %, чем в случае, если в качестве критерия выбора границ струи принято условие f(±b/2)=0,2.

Выражение (6) можно записать в следующем виде:

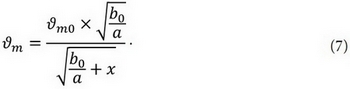
Тогда при условии

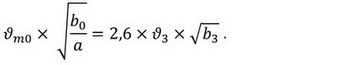
выражения (1) и (7) оказываются идентичны и отличаются лишь тем, что смещены друг относительно друга по оси x на расстояние b₀/a (рис. 6).

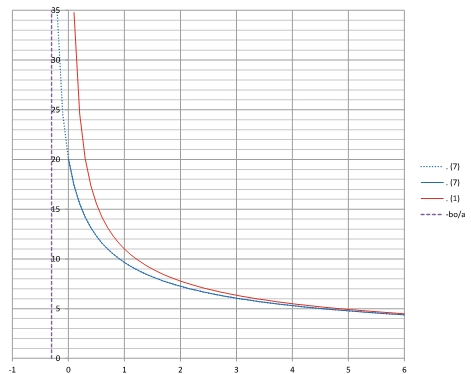
Рис. 6. Сравнение выражений (1) и (7) для максимальной скорости на оси струи

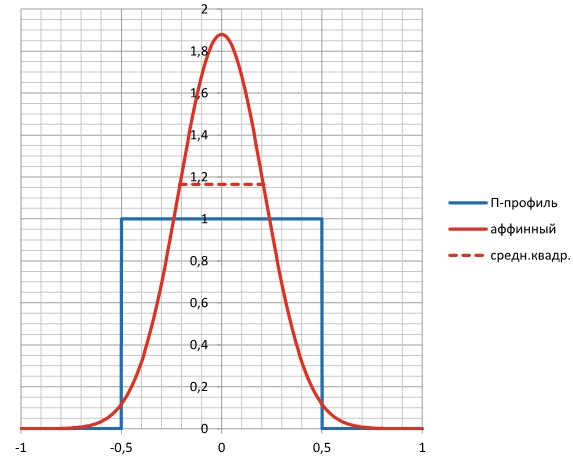
Рис. 7. П-образный и аффинный профили скоростей струй с одинаковыми значениями средних скоростей и одинаковыми значениями количеств движения секундных масс воздуха. Уровень «средн. квадр.» определяет значение среднеквадратичной скорости аффинного профиля струи

По сути, выражение (1) описывает зависимость значения максимальной скорости на оси аффинной струи с некоторым конечным значением количества движения секундной массы воздуха, но с бесконечно малой начальной толщиной струи b0 и соответственно бесконечно большим значением начальной максимальной скорости на оси струи ϑ_m0. По этой причине зависимость (1) на малых расстояниях от сопла завесы начинает вести себя неадекватно.

На рис. 7 представлены П-образный начальный профиль скоростей и аффинный нормально-распределенный профиль скоростей, имеющие одинаковые начальные толщины струи и одинаковые средние скорости (в качестве критерия полуширины аффинной струи принято расстояние между значениями скоростей в половину от максимальной скорости на оси). При П-образном профиле скоростей в сечении струи значения среднеквадратичной скорости и средней скорости совпадают. В то время как для профиля аффинной струи, как уже было отмечено ранее, они отличаются друг от друга в (0,38/0,28)^0,5 раз. Поэтому количество движения секундной массы воздуха струи с аффинным профилем скоростей на 35 % больше, чем у струи с П-образным профилем скоростей с тем же самым значением средней скорости. Соответственно они должны иметь разные графики поведения для максимальной скорости воздуха на оси струи. Однако с точки зрения формулы (1) их графики поведения идентичны, так как одинаковы входящие в формулу (1) начальные средние скорости и начальные толщины струи. Профили реальных струй воздушных завес чаще всего близки к П-образным, поэтому различие средней скорости и среднеквадратичной скорости для них обычно невелико. Например, зафиксированное максимальное различие между средней скоростью и среднеквадратичной скоростью среди 11 верифицированных завес составило 4,5 %. Но тогда, используя в выражении для максимальной скорости воздуха на оси струи значение средней скорости вместо среднеквадратичной скорости в начальном сечении струи, следует быть готовым, что отклонение расчетной зависимости от реальной может оказаться значительным и таким образом экспериментальные данные могут войти в противоречие с рассчитанными по формуле (1).

Как уже отмечалось ранее, модели завес разных производителей имеют свои уникальные профили распределения скоростей в начальном сечении струи. Но по мере продвижения вдоль струи все они приобретают одинаковую или подобную аффинную форму, соответствующую их количеству движения в начальном сечении струи. Струи завес, имеющие разные начальные профили скоростей, но совпадающие сформировавшиеся аффинные профили на некоторых расстояниях от начала струи, с этих расстояний должны иметь одинаковые отсечные свойства. Если для некоторой струи завесы известны толщина струи и максимальная скорость в сформировавшемся аффинном профиле в сечении на некотором расстоянии от начала струи, то можно рассчитать, каковы были бы толщина струи и максимальная скорость в начальном сечении (приведенная толщина струи и приведенная максимальная скорость), если бы струя с самого начала была бы аффинная. Эти приведенные параметры струи должны однозначно определять отсечные свойства завесы, и таким образом появляется принципиальная возможность сравнивать завесы друг с другом по отсечным свойствам.

В качестве обобщения вышеизложенного можно отметить следующее.

В выражении для максимальной скорости воздуха на оси струи отсчет расстояния до рассматриваемого сечения более корректно производить не от начала струи, как в выражении (1), а от полюса струи, находящегося в отрицательной области оси струи.

Также в выражении для максимальной скорости воздуха на оси струи правильнее использовать не значение средней скорости в начале струи, а значение среднеквадратичной скорости воздуха, то есть корень из среднего от квадрата скорости воздуха в начале струи. Тем более что при известном распределении значений скорости в сечении струи средняя скорость и среднеквадратичная скорость считаются одинаково просто.

Учитывая, что значение параметра расширения струи зависит от выбора граничных условий профиля скоростей в сечении струи, при предоставлении формул и выражений для воздушной струи следует указывать, по какому критерию определялась толщина струи.

Помимо имеющихся параметров значения ширины сопла завесы и среднеквадратичной скорости в начале струи, видимо, следовало бы ввести параметры приведенная начальная толщина струи и приведенная максимальная скорость на оси струи, которые имела струя, если бы с самого начала была аффинной. Тогда появилась бы возможность сравнивать завесы между собой по их отсечным свойствам.

Литература

1. Ослабление струи воздушной завесы (по результатам верификации). Лысцев С. А. Журнал «МИР КЛИМАТА» № 80.

2. Мнение Марр Ю. Н. о статье Лысцева С. А. «Ослабление струи воздушной завесы (по результатам верификации)». Журнал «МИР КЛИМАТА» № 80.

3. Абрамович Г. Н. Теория турбулентных струй. Репринтное воспроизведение издания 1960 г. — М.: Эколит, 2011.

Обмен мнениями

А. В. Пухов, инженер компании «Тропик»:

— В статье, посвященной затопленным воздушным струям, подробно разбирается случай неограниченной по краям плоскопараллельной струи. Приводятся значения скорости струи v в точках (х, у) в зависимости от начальной скорости v₀.

Применяемое автором моделирование позволяет получить величину скорости в зависимости от координаты «у». В центральной плоскости струи (у=0) приводятся значения максимальной скорости v_m на удалении «х», получаемые из сохранения полного потока импульса по мере распространения струи.

Упрощенные модели являются первым приближением для реальных физических процессов и указывают направление для их детального описания. «МИР КЛИМАТА» ориентирован на широкую аудиторию, и такие рассмотрения будут интересны как читателям, проявляющим интерес к данной тематике, так и специалистам в этой области. Последние получат возможность под иным углом зрения рассмотреть эту область физики, найти для себя новые и интересные соотношения между привычными физическими величинами.

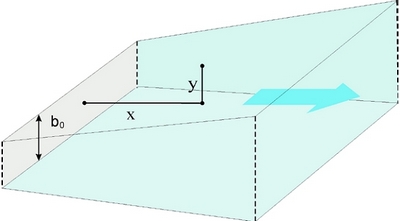
Распространение воздушной струи

В статье сделаны несколько допущений. Чтобы узнать, являются ли они произвольными или естественными ограничениями на поведение струй воздушных завес, воспользуемся методом размерного анализа и его рабочим инструментом π-теоремой. Для рассмотренного случая она непосредственно позволит получить и условия применения метода гидродинамического подобия для воздушных струй. Любой физический процесс можно описать определенным набором переменных, измеряемых в некоторых эталонных величинах или их отношениях. Например, для измерения скорости могут быть использованы единицы м/с, км/ч или другие. Очевидный факт заключается в том, что процесс будет происходить независимо от выбора единиц и его разные числовые представления, связанные с размерностью, достаточно искусственны. Из этого затруднения можно выйти, если описывать процесс в характерных для него безразмерных величинах. Они будут реальными характеристиками процесса, а не зависящими от искусственно введенной размерности. Пусть таких независимых безразмерных переменных для некоторого процесса можно подобрать n: (α₁, α₂, … α_n). Тогда в соответствии со сказанным выше эти величины будут связаны некоторой зависимостью, например, F (α₁, α₂, … α_n) = 0. И хотя невозможно определить заранее вид функции F, закономерности природы устроены таким образом, что иногда любую из этих реальных переменных процесса можно выразить через произведение остальных, взятых в некоторых степенях. Также очень часто, но не всегда, одну или несколько переменных α₁, α₂, … α_n можно исключать из уравнения F (α₁, α₂, … α_n) = 0, поскольку они перестают влиять на процесс, в том случае, если они очень малы (или, соответственно, велики). Размерность любых физических величин можно представлять в виде: L M T с соответствующими степенями длины, массы и времени, которые записываются после символа обозначения основной размерности. А именно: представление скорости в этих обозначениях есть L1T (–1), ускорения L1T (–2), мощности L2M1T (–3), силы L1M1T (–2), площади L2, давления L (–1) M1T (–2)…

Прежде чем использовать π-теорему, рассмотрим несколько показательных примеров ее применения. Найдем, например, время разгона автомобиля мощностью 73 кВт (100 л. с.) до 100 км/ч. Характерная безразмерная переменная процесса — это мощность, умноженная или деленная на важные, влияющие на разгон физические величины, взятые в некоторых, неизвестных априори степенях. Разделим мощность (N) на массу автомобиля (m), чтобы из финального представления полностью исключить размерность массы, а из оставшейся части L2T (–3) исключим еще и L2, разделив ее на квадрат скорости (v²) L2T (–2). Остаток T (–1) для приведения к безразмерному виду умножим на характерное время процесса (τ) T1. Итак, искомая переменная для процесса разгона: Nτ/ (mv²). Основное уравнение π-теоремы, как легко убедиться, для этого случая можно представить в виде: Nτ/ (mv²) =k₁, где k₁ — некоторая безразмерная постоянная. Если считать, что k₁=1, а массу принять как 1500 кг, то, учитывая, что 100 км/ч — это 27,8 м/с, можно получить τ = 15,9 с.

Найдем теперь максимальную скорость этого автомобиля. Можно предположить, что основную роль теперь будет играть сопротивление воздуха движению. Разделим мощность на величину плотности воздуха (ρ) L (–3) M для исключения размерности массы. Оставшийся размерный остаток L5T (–3) для исключения размерности времени разделим на куб скорости (v³) L3T (–3). Оставшееся выражение при делении ее на величину размерности L2 станет безразмерным. Из соображений физического смысла L2 — это площадь поперечного сечения автомобиля S. Таким образом, безразмерная переменная есть N/ (ρv³S). Запись π-теоремы для этого случая эквивалентна следующей: N/ (ρv³S) =k₂. Принимая k₂=1, плотность 1,2 кг/м³, а площадь 2,5 м², получим скорость 29 м/с, или 104 км/ч. Расхождение с современной реальностью здесь обусловлено тем, что k₂ — это коэффициент аэродинамического сопротивления. Принимая 0,3 в качестве его значения для современного автомобиля, получим его максимальную скорость равной 158 км/ч.

Можно заметить, что при решении этой задачи была пропущена другая безразмерная комбинация, а именно: N/ (v²ℓμ), ℓ — характерный линейный размер (может быть длиной автомобиля), μ — динамическая вязкость воздуха размерности L (–1) M1T (–1). За счет малого значения вязкости воздуха k₃ будет иметь очень большое значение и по причинам, указанным выше, не будет определять характеристики процесса. Тем не менее в некоторых случаях эта безразмерная переменная будет единственной характеристикой процесса, для которого π-теорема позволит записать выражение для мощности в виде N = k₃v²ℓμ. Это несколько иная запись хорошо знакомой формулы Стокса для медленных движений тел в вязких средах. Отметим, что для точного решения задач методом размерностей необходимо точное знание F (или коэффициентов k для случаев исключительного влияния одной переменной).

После представления метода размерностей перейдем к рассмотрению допущений статьи. Прежде всего будем считать рассматриваемые струи изотермическими. В применении к воздушным завесам это условие не выполняется, потому что воздушные завесы чаще всего используются для разделения воздушных сред различных температур и обычно в них используется дополнительный нагрев воздушной струи. Однако общим практическим правилом является, что изотермические струи воздушных завес характеризуют и потенциал температурного разделения сред воздушной завесой. На верификационных испытаниях воздушных струй завес в АПИК также исследуются изотермические струи и дополнительный нагрев воздуха не используется. Итак, перечислим все возможные независимые безразмерные комбинации переменных: v (x, y) /v₀, x/b₀, y/b₀, ρ₀v₀²/P₀, v₀/v_s, xv₀/ν. Две последние комбинации называются числами Маха М и Рейнольдса Re соответственно. P₀, — внешнее давление, ν — вязкость воздуха, v_s — скорость звука в воздухе, она связана со средней скоростью молекулярного движения и зависит от температуры. Заметим, что переменные х/у, ρ₀v²/P, v/v_s или другие подобные не являются независимыми, а могут быть выражены через уже перечисленные переменные. Утверждение π-теоремы для рассматриваемого случая заключается в том, что должна существовать некоторая неизвестная пока и, возможно, достаточно сложная функция F шести переменных, такая что F (v/v₀, x/b₀, y/b₀, ρ₀v₀²/P₀, M, Re) =0 является уравнением связи интересующей нас усредненной компоненты скорости v в соответствующих точках (х, у) со всеми другими параметрами этой задачи. Число Маха М для рассматриваемых нами случаев не превышает 0,06. При этом относительное изменение плотности воздуха Δρ/ρ₀ = 1/2М² < 0,0018 [1], то есть можно полностью пренебречь эффектами сжимаемости вещества. Таким образом, М и все связанные с ним звуковые влияния можно исключить из финального уравнения.

Рассмотрим влияние наружного атмосферного давления, обусловленное переменной ρ₀v₀²/P₀. Принимая атмосферное давление равным 100 кПа, плотность воздуха — 1,2 кг/м³, а максимальную воздушную скорость — 20 м/с, получим максимально возможное значение этой переменной 0,005. Эту переменную можно представить как ΔP/P₀ — отношение динамической части давления к полному давлению. Настолько малое значение параметра показывает, что распространение воздушной струи завесы можно с очень высокой точностью рассматривать как изобарический процесс и опустить эту переменную. Как следствие этого — полный поток импульса струи сохраняется (второе допущение статьи).

Если бы динамическая часть давления была бы сравнима с полной, то поток импульса струи не мог бы сохраняться. Очень просто это показать для ламинарных течений. Действительно, для небольшой трубки тока уравнение Бернулли для несжимаемой среды ρv₀²/2+P=const, выражающее постоянность суммы давления и плотности кинетической энергии потока, можно представить в виде: ρv₀²+2P=const. То есть сумма плотности потока импульса и удвоенного давления постоянна, что подразумевает несохранение потока импульса при изменении давления. Для турбулентных струй связь изменения потока импульса с изменением давления сохраняется.

Параметр Re определяет, какой именно характер течения реализуется — ламинарный или турбулентный. Критерий турбулентности — это значения Re, большие нескольких тысяч. Если принять скорость 20 м/с, а вязкость воздуха 1,5•10^-5м²/с, то получим, что в 50 см от начала струи значение Re превышает 5•10⁵, то есть мы имеем дело с развитой турбулентностью. Сам этот факт является ключевым для возможности изучения струй. Дело в том, что только при турбулентных случаях Re перестает оказывать заметное влияние на поведение струи [1]. С учетом сделанных выше выводов уравнение для искомой скорости можно представить как: F (v/v₀, x/b₀, y/b₀) =0 или в еще более удобном виде: v=v₀f (x/b₀, y/b₀). При значениях Re, соответствующих турбулентным течениям, возникает и еще одно значительное упрощение, а именно, начиная с некоторого значения «х» (на так называемом основном участке): струя становится автомодельной. А именно: при преобразовании координат x kx, y ky (k – некоторое число), отношение v (x, у) /v (х,0) сохраняет свое значение. Это свойство в статье обозначается эквивалентным термином «аффинность». Автомодельность при больших значениях Re — это экспериментальный факт (см. например [1, 2]). Из этого следует, что форма расширения струи линейна. То есть для изобарических несжимаемых турбулентных струй (каковыми и являются струи воздушных завес) допущения 2, 3 и 4, приведенные в статье, являются естественными условиями.

Турбулентность является важным условием для автомодельности струи, которая не реализуется в ламинарном случае. Задачу осесимметричной ламинарной затопленной тонкой струи впервые рассмотрел Лев Ландау (1943) [2]. Поверхности, образованные полем скоростей, в этом случае имеют достаточно сложный вид, который к тому же зависит от значения Re. Интересное отличие от турбулентного случая заключается и в том, что в движении участвует воздух и в зоне отрицательных значений х.

В качестве функции зависимости скорости от координаты «у» у автора принимается нормальное Гауссово распределение. Отметим, что данный вид распределения по «у», как и формула типа (1), зависимости от «x» является точным решением уравнений Навье — Стокса для струи, образованной бесконечно тонкой щелью, при всех сделанных выше оговорках относительно несжимаемости, изобаричности и турбулентности. Единственная трудность дальнейшего теоретического исследования даже этого наиболее упрощенного случая заключается в том, что и коэффициент при у-распределении и константа пропорциональности при х-зависимости не могут быть выведены теоретически, а определяются углом расхождения струи. Поскольку теория турбулентности полуэмпирическая, не существует другого способа его определения кроме экспериментального [2]. Этот угол, как отмечалось в статье, не имеет конкретного численного выражения, а зависит от критерия границы струи.

Для проверки результатов статьи и определения точной зависимости f (x/b₀, y/b₀) существуют мощные программные средства расчета, например, ANSYS FLUENT [3]. Их использование разрешило бы еще один важный вопрос, поднятый в статье. Для П-образного профиля, как было показано выше, существует единственная функция f (x/b₀, y/b₀), которая определяет поведение скорости в различных точках. Задавая программно профили, отличные от П-образного, можно будет строго обосновать приведенную в статье гипотезу автора о предпочтительном влиянии на сформировавшуюся струю именно среднего квадрата начальной скорости струи. Также можно будет получить критерии расстояний «х» от начала струи, на которых стираются различия между П-образными начальными струями и иными, с теми же средними квадратами начальных скоростей.

Литература

1. Теория пограничного слоя. Герман Шлихтинг. — М.: Наука1974.

2. Гидродинамика. Том 6. Теоретическая физика. Л. Д. Ландау, Е. М. Лившиц. — М.: Наука, 1986.

3. www.ansys.com.