- Главная
- Методики и расчеты
- Мощность тепловой завесы при произвольных расходах теплоносителя и воздуха. (Практическое применение теории. Продолжение). А.В. Пухов, ООО "Тропик-Лайн"
Мощность тепловой завесы при произвольных расходах теплоносителя и воздуха
Практическое применение теории
Эта статья завершает цикл статей [1], [2], посвященных исследованию тепловой мощности воздушных завес с жидким теплоносителем при произвольно заданных условиях их использования. В ней будут рассмотрены практические вопросы тепловых свойств этого типа воздушных завес. Так же, как в [1] и [2], будем обозначать Тг — температуру поступающей в теплообменник горячей воды, Тх — температуру обратной или холодной воды, Т0 — температуру окружающего воздушную завесу воздуха (начальную температуру воздуха) и
Т — усредненную конечную температуру воздуха на выходе из воздушной завесы. Воздушный и водяной расходы воздушных завес будем измерять в кг/с и обозначать как g и G соответственно. Статья состоит из нескольких разделов. Первый главным образом предназначен для потребителей воздушных завес, второй — для производителей, а третий фактически определяет, что ограничения применяемого подхода не являются существенными для стандартных случаев применения воздушных завес. В статье приводится формула для мощности воздушной завесы W как явной функции водяного и воздушного расходов при заданных Тг и Т0.
I. Для потребителей воздушных завес важным вопросом является регулирование тепловой мощности нагрева, в частности, ее возможное увеличение. Незапланированное уменьшение тепловой мощности может происходить из-за несоответствия реальных температур Тг расчетным, но главным образом вследствие уменьшения расхода G теплоносителя воздушной завесы по сравнению с предполагаемым. Причины, приводящие к уменьшению этого расхода, — это прежде всего последовательная схема подключения завес, большая длина подводящих магистралей и/или их недостаточное сечение, недостаточная производительность и/или напор насосов, использование в системе узлов недостаточного сечения. В некоторых случаях это приводит к существенному снижению расхода и, следовательно, передаваемой завесой мощности. Предложим наименее затратный способ диагностики ситуации с расходом теплоносителя и возможностей увеличения мощности до требуемых значений.
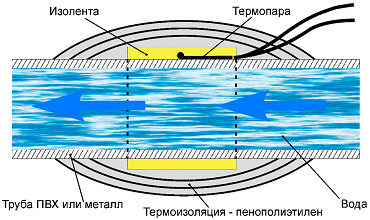 Рис. 1
Рис. 1
Так как для каждого теплообменного блока его мощность определяется расходом через этот конкретный блок, необходимо оценить степень расхода каждого интересующего теплообменного блока. Абсолютное значение расхода G кроме сложностей его измерения само по себе может определять степень его достаточности, только когда имеется дополнительная информация. Намного более точно степень достаточности расхода G может предоставить измерение Тх, которое можно произвести без вмешательства в водяную систему, например, с помощью термопары, накладываемой на выходную магистраль (рис. 1).
Эта же термопара впоследствии может быть использована как для нахождения Тх других теплообменных блоков, так и для определения температуры воды Тг, поступающей к каждому блоку или в общий коллектор. Далее полученное значение Тх сравнивается с температурами воздуха в месте установки данной воздушной завесы Т0 и температурой воды Тг, поступающей к этой же завесе. Если значение Тх оказывается заметно ближе к Т0, чем к Тг, то расход мал и обычно недостаточен, если значение Тх близко к значению Тг, то расход велик. Что касается потенциальной возможности увеличения мощности посредством увеличения расхода, то общее правило таково: чем ближе начальное значение Тх к Т0, тем больше возможностей для исправления ситуации малыми средствами. И напротив, если значения Тх и Тг близки, то увеличить мощность даже очень большими вложениями (конечно, не учитывая возможность замены воздушной завесы) практически невозможно. Эти рассуждения являются прямыми следствиями основной формулы теории, которая была представлена в [1], [2]:

Здесь С [кВт/К] — абсолютная способность воздушной завесы к передаче тепла,
а α — безразмерная величина, характеризующая степень влияния на теплопередачу значения перепада температур воды на теплообменнике ΔТW = Тг-Тх. Формула (1) при определенном воздушном расходе применима к широкой области изменения водяных расходов и совместно с основной формулой теплового баланса для этой же мощности:

позволяет связывать значения температур и мощностей при изменении условий работы воздушной завесы. В (2) численное значение множителя – это теплоемкость воды,
cW = 4,2кДж/ (кг•K). Предложим практические примеры оценки степени расхода воды:
1. Пусть для некоторой воздушной завесы, которая по ощущениям передает недостаточную величину тепловой мощности, с помощью измерения термопарой были получены следующие значения температур: Тг=92 °С, Тх=35 °С и Т0=18 °С. (Тг-Тх) >> (Тх-Т0) — расход недостаточен и возможно значительное увеличение тепловой мощности разумными средствами. После этой первоначальной оценки ситуации нужно найти непосредственную причину недостаточного расхода. Пусть инженерная экспертиза магистрали водоснабжения завесы показала возможность увеличения расхода в 2,3 раза. Хотя мы и не знаем значения α для этой завесы, для оценки примем его 0,1. Другие α будут приводить к близким значениям расчетов итоговой мощности завесы. В расчете на каждый киловатт мощности завесы из (1) найдем для данной завесы C1=0,044 [1/К] и из (2) расход G1=0,0042кг/ (кВт•с).
После увеличения расхода теплоносителя его новое значение будет составлять
G2=0,0096кг/ (кВт•с). Из (1) и (2) найдем новое значение температуры Тх2=51,2 °С и W2 = 1,64. Итак, мощность увеличена на 64 %.
2. Пусть для другой воздушной завесы, мощность которой также недостаточна, измерения термопарой привели к значениям температур Тг=92 °С, Тх=75 °С и Т0=10 °С. Так как
(Тг-Тх) << (Тх-Т0), то посредством увеличения расхода воды значительно поднять мощность не удастся. Тем не менее предположим, что было принято решение увеличить мощность посредством увеличения расхода теплоносителя G в 2,3 раза. Аналогичное рассмотрение приведет к значениям: G1=0,014кг/ (кВт•с), G1=0,0322кг/ (кВт•с), Тх2=83,8 °С и W2=1,11. В итоге получим незначительное увеличение мощности на 11 %. В проведении этих расчетов для принятия решения о возможности поднятия мощности нет необходимости, тем более что обычно невозможно предсказать точную величину увеличения расхода. Заметим, что нетрудно бывает поднять именно недостаточный уровень расхода, в то время как высокий расход поднимается крайне неохотно. Другое важное замечание касается возможного предела величины расхода через теплообменник. При увеличении расхода выше этого предела возможны различные нежелательные последствия, вплоть до физического разрушения теплообменного блока.
II. Последующее практическое рассмотрение большей частью предназначено производителям воздушных завес. Оно будет касаться возможностей описания тепловой мощности для любой воздушной завесы. Хотя существуют программы, которые позволяют выражать мощность воздушных завес при заданных условиях, в дополнение к ним можно использовать закономерности аналитического вида. Они дают возможность простого расчета и быстрой оценки значений тепловых параметров и их изменений при изменении условий, а также возможности независимой проверки опытных и табличных значений, применения моделей с различной степенью точности в зависимости от условий и требований.
1. Алгоритм проведения измерений, который позволяет получить полную информацию о произвольной воздушной завесе. Согласно результатам [2] предложим алгоритм измерений, которые нужно провести, чтобы определять мощность при любых условиях. В некотором смысле этот алгоритм менее строгий, чем Методика верификации воздушных завес [3]. Для измерений нужно сначала установить максимально возможный расход воздуха, который обозначим g1. При этом расходе нужно измерить тепловые мощности завесы при двух значениях расхода теплоносителя: среднем, когда Тх ≈ 1/2 (Тг+Т0) и достаточно большом, когда Тх ≈ 1/4 (3Тг+Т0). Оба расхода выставляются для приблизительного равенства Тх указанным значениям, например, с помощью регулировочного вентиля (хотя выбор этих температур может и отличаться от предложенного). При каждом из этих двух расходов нужно измерить, теперь уже с высокой точностью, их значения G, а также Тг, Тх и Т0. Затем из измеренных температур вычисляются две разности — главная опорная ΔТ0=Тх-Т0 и перепада температур воды на теплообменнике
ΔТW=Тг-Тх — и из (2) рассчитывается мощность. Если значения для одного измерения обозначаются индексом 1, а для другого — 2, то выражения
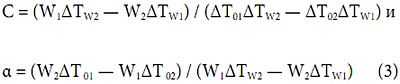
будут определять тепловые свойства завесы при этом расходе воздуха уже для любых расходов теплоносителя (в смысле условий применимости, которые подробно будут обсуждаться ниже), а выражение (1), в котором С и α2. И наконец, обозначим полученные величины (3) для первого из воздушных расходов g1 как С1 и α1, а для второго g2 — как С2 и α2, они будут использованы для вычисления C (g) и α (g).
2. Нахождение значений тепловой мощности завесы при произвольных расходах теплоносителя и воздуха на основе четырех проведенных измерений. Если рассматриваемая воздушная завеса имеет некоторое промежуточное значение воздушного потока или же плавную регулировку воздушного потока (например, частотную или с помощью управления двигателем постоянного тока), то для любого значения воздушного потока g мощность воздушной завесы будет определяться аналогом (1) (формулы (27) — (32) работы [2]):
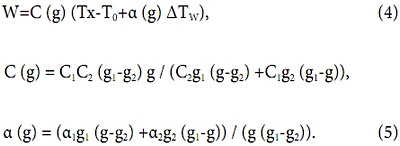
В (5) g можно измерять как в единицах массового [кг/с], так и объемного [м3/ч] расхода, поскольку квадраты расхода присутствуют как в числителе, так и в знаменателе (5).
3. Оценка достоверности полученных при измерениях значений тепловой мощности. Развитие теории теплообмена в воздушных завесах [2] позволяет использовать опубликованные или внутренние данные производителей для оценки точности измерений, при которых были получены эти данные. Ниже приведем алгоритм проверки, который может либо подтвердить достоверность опытных данных, либо указать на их недостаточную точность. В обоих случаях можно получить дополнительную информацию относительно рассматриваемой воздушной завесы. Предположим, что для некоторой воздушной завесы из опубликованных данных для двух воздушных расходов g1 и g2 рассчитаны значения С1, α1, С2 и α2. По формулам [2] рассчитаем следующие коэффициенты:
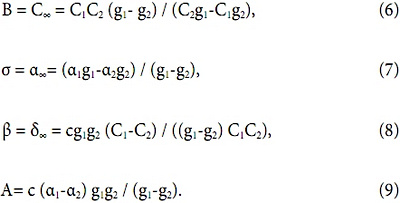
В — это основной коэффициент, указывающий абсолютную способность к передаче завесой тепла, σ, β и А определяют все многообразие процесса теплопередачи, но их совместное влияние на величину теплопередачи не превышает 10–20 %. Обычно σ и (1-β) — это достаточно малые положительные величины, что указывает на то, что теплопередача в основном пропорциональна разности температур горячего воздуха и холодной воды (Т-Тх), А — это отрицательный, очень малый по своему абсолютному значению коэффициент. Результаты расчета этих 3 коэффициентов могут определить степень достоверности исходных данных мощностей для различных условий. Поясним это примерами: рассчитаем постоянные (6) — (9) для двух воздушных завес разных производителей. Для первой из них для нахождения значений С1, α1, С2, α2 по (3) использованы табличные данные, для другой — данные по теплообменному блоку. Результаты расчета по всем коэффициентам представим в виде табл. 1.
Таблица 1
| Воздушные завесы | g1, кг/с | g2, кг/с | C1, кВт/К | C2, кВт/К | α1 | α2 | Ϭ | B, кВт/К | β | A, кВт/К | g1с/Bβ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0,810 | 0,354 | 0,651 | 0,342 | 0,285 | 0,38 | 0,211 | 2,180 | 0,877 | -0,06 | 0,43 |
| 2 | 0,777 | 0,565 | 0,498 | 0,407 | 0,136 | 0,15 | 0,099 | 1,232 | 0,934 | -0,029 | 0,68 |
Как можно видеть, значения σ малы по сравнению с 1 и положительны, значения β несколько меньше 1, А — малы и отрицательны. Все знаки и значения этих величин находятся в непротиворечивой связи с физическим смыслом этих величин, из чего можно заключить, что во время измерений тепловых мощностей для этих воздушных завес или теплообменников не было допущено грубых ошибок. Можно привести примеры опубликованных данных для мощностей воздушных завес, приводящие к таким значениям С1, α1, С2, и α2 по (3), что соответствующие им σ, β и А противоречат физическому смыслу и могут являться основанием для уточнения значений мощностей. Например, при β > 1 мощность воздушной завесы была бы пропорциональна разности между некоторым значением водяной температуры и значением воздушной температуры, превышающим значение температуры нагретого воздуха Т, и не может ни при каких условиях являться «характерной» воздушной температурой теплообмена. Небольшие отклонения коэффициентов от указанных областей могут свидетельствовать о незначительных погрешностях измерений.
4. Оценка соответствия максимального воздушного расхода воздушной завесы своему оптимальному значению. Значение коэффициента В может быть использовано для оценки оптимального значения воздушного расхода завесы. Значение максимального конструктивного воздушного расхода g1 можно сравнить с «характерным» расходом воздушной завесы
g0 = βВ/с [2]. Это отношение для каждой воздушной завесы есть строго определенная величина, которая связывает конструктивный воздушный расход завесы и способность теплообменного блока к передаче тепловой мощности. Обычно значение g1/g0 для воздушных завес находится в пределах 0,6÷0,9 со средним значением около 0,75. Если значение расхода выходит за указанные границы, то можно считать, что расход g1 мал (способность к теплопередаче далека от выхода на режим насыщения) или велик (воздушный расход находится в области насыщения теплопередачи). Для рассмотренных выше завес значения параметров g1с/βВ, считая, что теплоемкость воздуха с=1,005 кДж/кгК, равны соответственно 0,43 и 0,68 (табл. 1). Можно сказать, что первая завеса имеет недостаточный конструктивный воздушный расход, который не позволяет использовать потенциал теплообменника оптимальным образом. Можно оценить и максимальное значение необходимого расхода теплоносителя [2] для этих воздушных завес как Gmax ≈ В/cW, что дает для них значения Gmax, равные 0,519 кг/с и 0,293 кг/с. (Формула для Gmax вытекает из предположения, что в оптимальном режиме работы завесы для изменений водяной и воздушной температур справедлива оценка ΔTW ≈ ΔT. Тогда из уравнения теплового баланса следует приблизительное равенство водяного и воздушного тепловых эквивалентов g0с ≈ GmaxcW, и, учитывая, что β ≈ 1, получим Gmax ≈ В/cW.)
5. Разные варианты вида формул расчета мощности для воздушных завес. Допустим, что по проведенным измерениям или из табличных данных, используя (3) для двух воздушных расходов g1 и g2, рассчитаны значения С1, α1, С2, и α2. Тогда, как было указано выше, для нахождения мощности уже при любых расходах g, необязательно совпадающих с g1 и g2, можно применить формулу (4), коэффициенты которой определяются соотношениями (5). Используя (2), эту формулу можно представить несколькими эквивалентными формами записи:
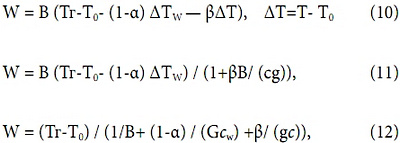
где α, В, β определяются соотношениями (5), (6), (8). Для разных задач можно выбирать наиболее удобную форму записи. Заметим, что (4), (10) — (12) являются точными в смысле логики теории [1], [2], а (12) с учетом α (g) =σ+A/ (cg) [2] к тому же является выражением тепловой мощности как явной функции лишь водяного и воздушного расходов. Ее кажущуюся асимметрию по расходам G и g можно опровергнуть приведением выражения (12) к виду:
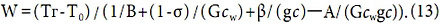
Соотношения (4), (10) — (13) отражают факт наличия 4 степеней свободы в системе теплообмена, который может быть выражен различными наборами определяющих коэффициентов, например (С1, α1, С2, α2), (В, β, α1, α2) или (В, β, σ, А).
6. Варианты упрощения формул расчета. Если считать А (самую малую из набора констант 1-β, σ, А) нулем, А≡0, то можно упростить формулы для мощности. В этом случае в (10) — (13) в качестве α можно использовать некоторое среднее значение, например α0= (α1+α2) /2.
Следующая степень упрощения — это пренебрежение не только изменениями α, но и самим его значением: А≡0, σ≡0. Формулы мощности (10) — (13) для этого случая примут вид:
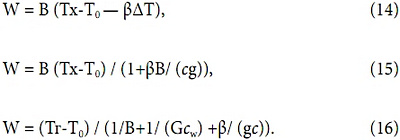
Для описания тепловых свойств в этом приближении достаточно проведения двух измерений мощности при разных значениях воздушного расхода g1 и g2 и при некоторых значениях водяного расхода G. Из (15) следует, что для любого фиксированного воздушного расхода g, возможно, и не равного значениям g1 и g2, это приближение сведется к выражению однопараметрического подхода, который был предложен Сергеем Анатольевичем Лысцевым (см., например, [4]). Роль основного параметра этого подхода Ск будет играть следующая функция воздушного расхода g:

Выражение (15) с учетом (17) — это основное соотношение однопараметрического подхода:

В [4] (18) приводится в виде W=4,2Дж/кгК•Ск (Тх-Т0) для измерения коэффициента Ск в единицах расхода кг/с, а изменений воздушного расхода не подразумевается, в то время как (18) в общем случае подразумевает произвольный воздушный расход, а (17) обозначает явную зависимость Ск от g. Можно обратить выражение (17) в смысле поиска значений В и β по двум значениям Ск, рассчитанным для двух воздушных расходов:
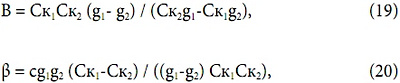
Ск1 и Ск2 — это значения параметра Ск при расходах g1 и g2. Приближение (18) применимо в области и средних и высоких расходов, когда В и β вычислены для области умеренно высоких расходов G. Представим расчет В и β по (19) и (20) для двух рассмотренных выше воздушных завес в этом приближении для условий (95/70 при 15) в виде табл. 2.
Таблица 2
| Воздушные завесы | g1, кг/с | g2, кг/с | Cк1, кВт/К | Cк2,кВт/К | B, кВт/К | β | gс/Bβ |
|---|---|---|---|---|---|---|---|
| 1 | 0,81 | 0,354 | 0,735 | 0,401 | 2,08 | 0,72 | 0,55 |
| 2 | 0,777 | 0,565 | 0,529 | 0,435 | 1,25 | 0,85 | 0,74 |
Можно считать этот вид упрощения вычислений обобщением Ск подхода [4] для произвольных значений воздушного расхода. Он дает высокую точность при всех значениях воздушного расхода и для некоторых изменений расхода теплоносителя. Для примера вычислим точные значения мощности для двух выше-указанных завес по (4) и (5) для воздушного расхода g=0,6 кг/с (предположим эти возможности для воздушных завес 1 и 2) и условий «95/65 при 15». Они равны для первой и второй завес соответственно W1=29,33 кВт и W2=21,24 кВт. Теперь же воспользуемся приближенным расчетом (17), (18) со взятыми из табл. (2) значениями В и β, тогда W1=26,87 кВт и W2=20,36 кВт. Видно, что завеса 1 с большими α имеет погрешность в измерении мощности около 8 %, в то время как завеса 2 с умеренным α — лишь 4 %. Этот диапазон погрешностей приемлем для большинства практических задач. Но этим методом нельзя пользоваться для оценки достаточности воздушного расхода завесы посредством параметра cg/βВ, поскольку в этих оценках всегда присутствуют искаженные значения β, компенсирующие приближение Ск метода (А≡0, σ≡0).
Ограничения теории. 1. Рассмотрим с практической точки зрения ограничение на величину расхода G, которое было представлено в работах [1], [2]:

на величину расхода воды. Кратко напомним смысл ограничения (21): выражения для мощности, принятые в данном цикле статей, расходятся при значении расхода G = С1α1/cW, откуда следует, что они имеют смысл лишь при G, значительно больших величины С1α1/cW. С другой стороны, в [1] и [2] на основании экспериментальных и расчетных данных показано, что для расходов G, начиная с 3С1α1/cW и выше, и экспериментальный материал и программные расчеты с высокой точностью соответствуют теории [1] и [2]. Итак, вернемся к практическому значению (21). Для некоторой воздушной завесы будем считать, что при максимальном воздушном расходе g1 и условиях достаточно большого водяного расхода теплоносителя (например, при Тг = 95 °C,
Тх=85 °С и Т0=15 °С) ее тепловая мощность равна W1 [кВт]. Тогда из (2) получим расход теплоносителя для этих условий G1=0,0238W1 кг/(кВт•с). Это означает, что при перепаде
ΔТW=10 °С на каждый киловатт мощности воздушной завесы потребуется 0,0238 кг/с расхода теплоносителя. С другой стороны, из выражения для мощности воздушной завесы (1):
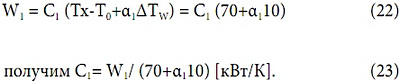
Чтобы полностью доопределить воздушную завесу, достаточно задать для этого воздушного расхода и значение α1, которое мы примем сначала достаточно малым α1=0,05. Таким образом, мы опишем широкий класс воздушных завес с малыми α. Если α1=0,05, то из (23) значение
C1 = 0,0142 кВт/К. Коэффициенты C1 и α1 определяют мощность данной воздушной завесы для этого воздушного расхода при любых изменениях водяного расхода G ≥ G0, который из (21)
G0 = 0,00051 кг/(кВт•с) (заметим, что G0 в этом случае в 47 раз меньше, чем G1). Чтобы найти значение температуры Тх, которая реализуется при расходе G0, нужно приравнять выражения для мощности (1) и (2) с указанными выше значениями G0, C1 и α1:
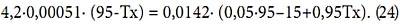
Решая это уравнение относительно Тх, получим Тх=22,3 °С (при этом тепловая мощность W=0,155W1, то есть более чем в 6 раз меньше первоначального значения). Для любых расходов больших G0=0,00051 кг/кВт•с и любых температур холодной воды выше Тх0=22,3 °С теория [1], [2] полностью применима для завес с настолько малыми значениями α1. Если же теперь рассмотреть класс завес с α1=0,2, то аналогичные рассуждения приведут к применимости теории до значений G0=0,0020 кг/кВт•с, Тх0=38 °С. Если же допустимы систематические погрешности в выражении для мощности до нескольких процентов, то можно применять теорию и до значений G > 3/4G0, то есть до еще более низких значений Тх.
Что же произойдет, если для этих завес расход еще уменьшить? Выражения теории [1] и [2] в этом случае перестанут работать, постоянное значение C1 потеряет смысл (оно будет плавно уменьшаться при дальнейшем уменьшении расхода). Например, для воздушных завес с α1=0,05 при уменьшении расхода G до значений заметно ниже критического G0=0,00051 кг/кВт•с температура Тх станет заметно ниже 22 °С, и мощность воздушной завесы можно с достаточной точностью определять выражением (2) в предположении Тх≡Т0. Модель, которая может описывать тепловые свойства воздушных завес при расходах G менее критических (возможно, до значений
G ≥ G0/3), была разработана Сергеем Лысцевым, с ней можно ознакомиться, например, в [4]. В этой работе автором были даны и очень удачные названия как модели [1], [2], (температурный подход), так и подходу при меньших расходах G (расходный). Действительно, при малых расходах (ТхТ0) разность (Тг-Тх) в (1) становится практически постоянной, однако можно еще многократно уменьшать мощность посредством уменьшения расхода. То есть, когда температурные возможности уменьшения мощности исчерпаны, в игру вступают расходные. В работах [1], [2] было указано, что ограничение на минимальный расход теплоносителя G не является существенным для практического применения воздушных завес. Действительно, на практике потребители завес должны стремиться к расходам выше средних, когда Тх ≥ (Тг+Т0) /2.
2. Ограничение модели теплового подобия. Использование перегретой воды. В этом цикле статей для расчетов тепловой мощности при различных температурах подразумевалось строгое выполнение принципа температурного подобия. Не вдаваясь в подробное изложение этого предмета, поясним его примерами. Допустим, что нам точно известна мощность тепловой завесы при условиях «95/70 при 20», тогда мы знаем величину мощности при условиях «115/90 при 40» или, например, «85/60 при 10». А именно — мощности будут в точности такими же (воздушный расход во всех трех случаях одинаков). Этот тривиальный случай подразумевает одновременное поднятие всех трех температур на одинаковую величину. Очевидно, что и расход теплоносителя будет для всех этих случаев одинаковым. Несколько сложнее выглядит ситуация, когда сравниваются следующие условия работы воздушной завесы «60/40 при 20» и «80/50 при 20» (расход воздуха завесы одинаков). В этом случае всевозможные температурные разности увеличились в 1,5 раза. Соответственно мощность завесы увеличится в 1,5 раза при сохранении расхода G. Это наглядно демонстрирует уравнение (2). Ключевым моментом всех этих сравнений является неизменность расхода теплоносителя, а если точнее, сохранение некоторой характеристики, которую можно назвать «характер теплопередачи», обусловленный явлениями турбулентного переноса. Количественно теплопередача наряду с температурной разностью выражается некоторой функцией двух безразмерных чисел (Рейнольдса — Re и Прандтля — Pr). Если характер теплопередачи изменится, то даже при формальном сохранении величины расхода G точная пропорциональность эффективных температурных градиентов нарушится. В этом случае невозможно будет говорить не только о пропорциональности мощностей для случаев «60/40 при 20» и «80/50 при 20», но и о равенстве мощностей для случаев «95/70 при 20» и «85/60 при 10». Отметим, что обычно тепловые условия воздушной части завесы находятся в следующих пределах: Т0 = 10÷20 °С, Т = 30 ÷ 40 °С, то есть средняя эффективная температура воздуха не выходит за рамки значений 20 °С — 30 °С. Иная картина наблюдается со значениями температур воды — средняя температура может быть как 40, так и 90 °С, например, при температурном перепаде 110/70. Течение теплоносителя в теплообменном блоке можно приближенно представить как течение жидкости в трубке некоторого радиуса. Для этого случая академик Михеев М. А. приводит критерий теплопередачи [5], который при условии постоянства температуры стенки трубы может быть приведен к виду:

Найдем табличные значения числа Прандтля для воды при температурах 90 и 40 °С и представим их отношение Pr90/Pr40 =1,963/4,338 = 0,4525. Отношение чисел Рейнольдса для указанных температур представим как обратное отношение кинематических вязкостей воды
Re900/Re40 = ν40/ν90 = 0,658/0,326=2,018. Таким образом, изменение критерия (25) при увеличении средней температуры воды с 40 до 90 °С составляет величину 1,028. Итак, при указанном увеличении средних температур воды теория предсказывает незначительное 3 процентное увеличение мощности теплопередачи по сравнению со случаем строгого выполнения соотношений температурного подобия. Это согласуется с результатами программных расчетов, которые также демонстрируют незначительное относительное увеличение мощности теплопередачи при заметном увеличении температур воды. Таким образом, физические свойства воды позволяют применять выражения для температурного подобия в широком диапазоне температур. Если же в качестве теплоносителя используются другие жидкости, то априори говорить о достаточно точном выполнении критерия температурного подобия, как в случае с водой, нельзя.
Литература
1. Пухов А. В. Мощность тепловой завесы при произвольных расходах теплоносителя и воздуха. Интерпретация опытных данных. «МИР КЛИМАТА» № 80, Москва, 2013.
2. Пухов А. В. Мощность тепловой завесы при произвольных расходах теплоносителя и воздуха. Инварианты процесса теплопередачи в воздушных завесах. «МИР КЛИМАТА» № 82–83, Москва, 2014.
3. Обновленная методика верификации воздушных завес с водяным нагревом, «МИР КЛИМАТА» № 77, Москва, 2013.
4. Лысцев С. А., Принципы и подходы к расчету тепловых параметров воздушных завес. «МИР КЛИМАТА» № 83, Москва, 2014.
5. Михеев М. А., Михеева И. М. Основы теплопередачи. Изд. 2-е, стереотипное, М., Энергия, 1977.
