- Главная
- Методики и расчеты
- Мощность тепловой завесы при произвольных расходах теплоносителя и воздуха. (Инварианты процесса теплопередачи в воздушных завесах. Продолжение). А.В. Пухов, ООО "Тропик-Лайн". Журнал "Мир климата" №83
Мощность тепловой завесы при произвольных расходах теплоносителя и воздуха. Инварианты процесса теплопередачи в воздушных завесах. Продолжение
Эта публикация — продолжение статьи, напечатанной в журнале «МИР КЛИМАТА» № 82. Обе части материала имеют общий список литературы и сквозную нумерацию формул.
Чтобы подтвердить справедливость выражения (20), можно воспользоваться расчетной программой. В качестве примера приведем данные расчетной программы производителя теплообменных блоков ROEN EST SPA [4], используемых компанией «Тропик» для производства воздушных завес с жидким теплоносителем 400-й и 500-й серий. В программе каждому теплообменному блоку присваивается код, позволяющий рассчитывать его мощность при произвольно заданных условиях температур и расходов. Итак, выберем для каждого из этих теплообменников два фиксированных расхода теплоносителя, один из которых будет находиться в области больших расходов, а другой — в области средних. Для всех расчетов зададим температуру воды на входе Тг = 95 °C и воздушного окружения Т=15 °C. Для блока, который в этой программе имеет код 6.30.CU.10.AL.08.02.0743.21.W.X.X.004.014.R3/4˝L, зададим первое значение расхода воды G = 0,19 л/с. Результаты расчета тепловой мощности для области воздушных расходов от 1000 до 4000 м3/ч с шагом 500 м3/ч представим в виде табл. 1. Несистемные единицы измерения расхода воздуха м3/ч вместо кг/с выбраны по причине их распространенности в среде производителей и потребителей воздушных завес.
Таблица 1
| Расход воды G, л/с | 0,19 | 0,19 | 0,19 | 0,19 | 0,19 | 0,19 | 0,19 |
| Расход воздуха g, куб. м/ч | 1000 | 1500 | 2000 | 2500 | 3000 | 3500 | 4000 |
| Температура обратной воды Тх, C° | 78,5 | 74,8 | 72 | 69,8 | 68,1 | 66,6 | 65,3 |
| Температура воздуха на выходе Т, С° | 52,79 | 45,81 | 41,24 | 37,97 | 35,54 | 33,6 | 32,02 |
| Температура воздуха на входе Т0, С° | 15 | 15 | 15 | 15 | 15 | 15 | 15 |
| Рассчитанная тепловая мощность W, кВт | 12,81 | 15,67 | 17,78 | 19,46 | 20,88 | 22,06 | 23,07 |
Принимая δ=1,35, исходя из того, чтобы при больших g значения D не зависели от g, представим значения D=W/ (Тх– Т0–δΔТ), где ΔТ=Т– Т0, для каждого из значений мощности на графике 1. Приблизим на этом же графике эти значения D некой константой Deff (это приближение обозначено розовым цветом):
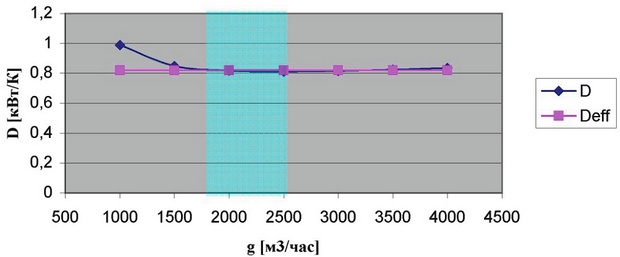
График 1
В таблице 2 представим программный расчет мощности для тех же условий и умеренного расхода воды G = 0,1 л/с.
Таблица 2
| Расход воды G, л/с | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 |
| Расход воздуха g, куб. м/ч | 1000 | 1500 | 2000 | 2500 | 3000 | 3500 | 4000 |
| Температура обратной воды Тх, С° | 68,2 | 63,4 | 59,8 | 57,6 | 55,6 | 53,8 | 52,6 |
| Температура воздуха на выходе Т, С° | 47,38 | 40,49 | 36,05 | 33,18 | 30,95 | 29,17 | 27,87 |
| Температура воздуха на входе Т0, С° | 15 | 15 | 15 | 15 | 15 | 15 | 15 |
| Рассчитанная тепловая мощность W, кВт | 10,98 | 12,96 | 14,26 | 15,4 | 16,21 | 16,81 | 17,43 |
Принимая δ=1,30, аналогично найдем D и представим полученные значения на графике 2.
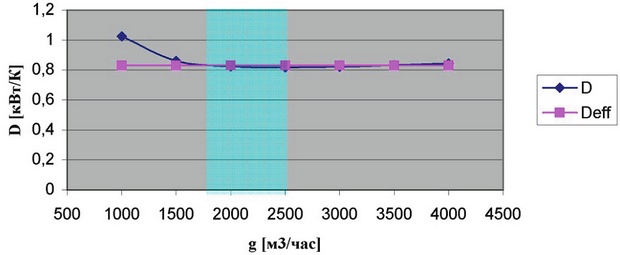
График 2
Области, заштрихованные на графиках, представляют интервалы допустимых воздушных расходов в воздушных завесах «Тропик» при использовании данного теплообменного блока.
Теперь рассмотрим блок с кодом 6.30.CU.10.AL.10.02.0931.21.W.X.X.005.018.R3/4˝. Для него зададим диапазон воздушных расходов от 1500 до 4500 м3/ч, чтобы отразить область его возможного использования. Результаты программного расчета для G = 0,2 л/с представим в виде таблицы 3.
Таблица 3
| Расход воды G, л/с | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 |
| Расход воздуха g, куб. м/час | 1500 | 2000 | 2500 | 3000 | 3500 | 4000 | 4500 |
| Температура обратной воды Тх, С° | 72,3 | 69 | 66,4 | 64,2 | 62,4 | 60,8 | 59,5 |
| Температура воздуха на выходе Т, С° | 51,39 | 46,31 | 42,61 | 39,75 | 37,49 | 35,62 | 34,1 |
| Температура воздуха на входе Т0, С° | 15 | 15 | 15 | 15 | 15 | 15 | 15 |
| Рассчитанная тепловая мощность W, кВт | 18,5 | 21,33 | 23,4 | 25,16 | 26,67 | 27,97 | 29,12 |
Для этой величины расхода воды, принимая δ=1,28, найдем D и представим полученные значения на графике 3.
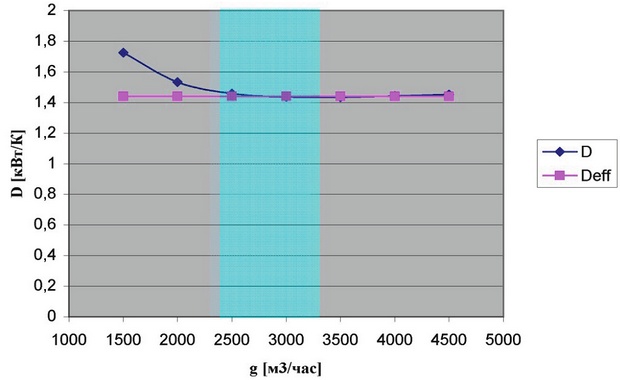 График 3
График 3
И наконец, для этого же блока примем достаточно большой расход воды, равный 0,32 л/с. Полученные результаты отобразим в таблице 4.
Таблица 4
| Расход воды G, л/с | 0,32 | 0,32 | 0,32 | 0,32 | 0,32 | 0,32 | 0,32 |
| Расход воздуха g, куб. м/час | 1500 | 2000 | 2500 | 3000 | 3500 | 4000 | 4500 |
| Температура обратной воды Тх, С° | 79,4 | 76,8 | 74,7 | 73 | 71,4 | 70,1 | 68,9 |
| Температура воздуха на выходе Т, С° | 54,86 | 49,86 | 46,11 | 43,24 | 40,88 | 38,93 | 37,33 |
| Температура воздуха на входе Т0, С° | 15 | 15 | 15 | 15 | 15 | 15 | 15 |
| Рассчитанная тепловая мощность W, кВт | 20,27 | 23,62 | 26,36 | 28,72 | 30,7 | 32,48 | 34,05 |
Принимая δ=1,31, найдем D и представим результаты в виде графика (см. график 4).
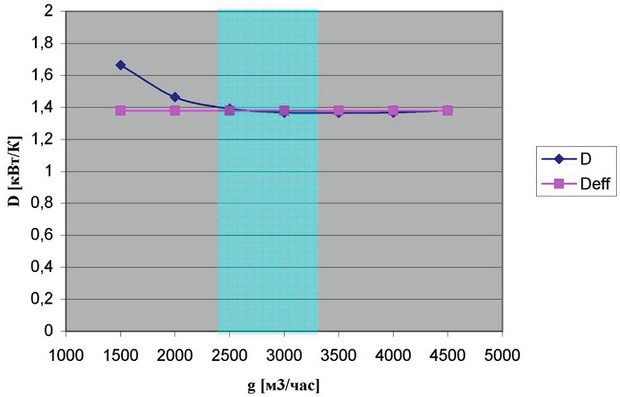
График 4
На каждом из вышеприведенных графиков представлены как программно рассчитанные коэффициенты D, так и приближения Deff для каждого из водяных расходов. Причем точность подобного приближения в каждом из случаев такова, что погрешность не превышает нескольких процентов в больших диапазонах воздушных расходов. Результаты других измерений и расчетов также подтверждают справедливость (17), хотя в данном цикле статей автор принципиально не использует полученные им самим результаты измерений в качестве исходного материала. Что касается области применимости (17), то, очевидно, она будет аналогична (3) с симметричной заменой водяных коэффициентов воздушными и в общем случае определяться соотношением (18). Однако вместо α в формуле оценки должно быть учтено не δ, а δ–1. Это определяется способом приведения выражения (19) к виду (20). Для области применимости (20) получим:

для каждого из значений водяного расхода, где с — это теплоемкость воздуха, приблизительно равная 1 кДж/ (кг•К). Вместо коэффициента 3 в формуле присутствует 2, поскольку соотношение для воздушного расхода менее строгое. Проверим это предположение для двух теплообменных блоков, рассмотренных выше. Для первого, принимая D ~ 0,8 кВт/К и δ ~ 1,3, получим область воздушных расходов g ≥ 0,48 кг/с или, что то же g ≥ 1500 м3/ч. Для второго D ~ 1,4 кВт/К и δ ~ 1,3 получим область воздушных расходов g ≥ 2600 м3/ч. Из приведенных графиков следует, что (20) выполняется с требуемой точностью в областях (21).
Теперь можно переходить к полностью формализованному математическому рассмотрению явлений теплопередачи в воздушных завесах. Будем везде далее считать, что индекс j определяет расход воздуха, а индекс k — расход воды. Тогда соотношение (4) можно представить в виде:

где ΔT0 обозначает разность Тх– Т0. Отсутствие индекса k у С и α означает их постоянство при изменении расхода воды. Представляя Δ ТW как W/ (Gkcw), получим:
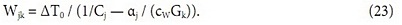
Аналогично соотношение (20) для мощности можно представить как:

с помощью замены и ΔT = W/ (gjc) его можно привести к виду:

Теперь в соотношениях (23) и (25) зафиксируем два различных расхода воды G1 и G2 при некотором произвольном расходе воздуха g и приравняем их. Эти равенства при каждом из этих расходов приведут к системе уравнений:
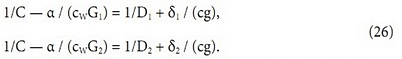
Решение этой системы позволит найти выражения для α и С:
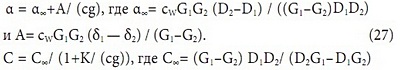
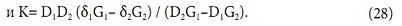
Допустим, в результате измерений нам удалось для двух воздушных расходов вычислить значения α1(G1) и α2(G2). Тогда, используя представление: α (g) = α∞+A/ (cg), найдем α∞ и A. Из

получим:

Далее, учитывая вид для С (g): С = С∞/ (1+K/ (cg)), найдем С∞ и K, по точкам С1(G1) и C2(G2):

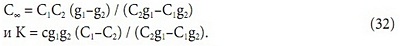
Вернемся к соотношениям (23) и (25) для нахождения зависимостей D и δ от расхода воды G. Для этого при произвольном расходе G зафиксируем теперь воздушные расходы G1 и G2 и, приравняв части (23) и (25), получим следующую систему уравнений:
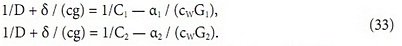
Применяя аналогичные рассуждения, получим:
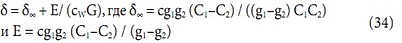
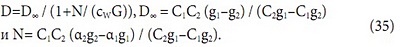
Решим систему уравнений:


и систему:
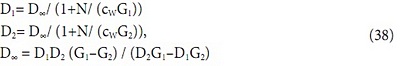
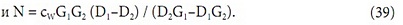
Сравнивая (32) и (35) или (28) и (39), получим D∞ = С∞ = В. Этот коэффициент (10) уже был получен в первой части статьи как В0. Не будем использовать дополнительный индекс, поскольку эта величина может принимать единственное значение для каждой воздушной завесы. Если в формулу для мощности (22) подставить W=cgΔT и Сj = B/ (1+K/ (cg)), получим:

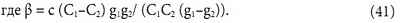
Если по аналогии в (24) подставить W=cwGΔT, D=B/ (1+N/ (cwG)), получим:

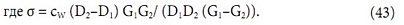
Формулы (40) и (42) являются разными представлениями выражения теплопередачи, причем коэффициенты (40) не изменяются при изменении расхода воды, а (42) — воздуха. Наряду с уже указанными равенствами D∞ = С∞ = В, заметим также, что:
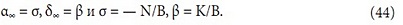
Можно поставить вопрос: сколько величин из набора A, σ, K, B, E, N, β независимых? Докажем, что только четыре. Действительно, пусть было произведено четыре измерения параметров работы некоторой воздушной завесы и для расходов G1 > G2 получены значения С1, α1, C2, α2. Покажем, что в этом случае мы знаем все вышеуказанные коэффициенты. Найдем α∞ = σ и A (30), С∞ = В и K (32), δ∞ = β и E (34) и N (35). Итак, степеней свободы не более четырех. Теперь допустим, что их три. Формула мощности близка именно к соотношению Wjk=B(ΔT0+σΔ ТW–βΔT). Пусть, например, величины B, σ и β у двух воздушных завес одинаковы. Могут ли эти завесы давать разную мощность при некоторых условиях? Пусть у одной из завес при двух расходах G1 и G2 α принимает значения α1 и α2 и α∞ = σ. Выберем вторую завесу с произвольным α1‘ > σ, α1‘ ≠ α1 при том же расходе G1 и α2‘ = α1‘G1/G2 — σ (G1–G2) /G2 при расходе G2. При таком выборе α1‘ и α2‘ σ второй воздушной завесы не изменится, однако A поменяет свое значение, что и доказывает различие тепловых свойств завес с почти одинаковым набором коэффициентов. То есть из набора инвариантов A, σ, K, B, E, N, β только четыре независимых. Что касается существования этих инвариантов, отметим лишь, что если при G1 > G2 набор значений С1, С2, α1, α2 удовлетворяет неравенствам C1 > C2, C2G1 > C1G2, α1 < α2 и α1G1 > α2G2, то все они не только существуют, но и имеют физический смысл.
Коэффициент α определяет степень влияния на теплопередачу перепада температур воды (см., например, [1]). С помощью (30) можно получить его значение при бесконечном воздушном расходе для любой воздушной завесы. В реальности бесконечного расхода, конечно, быть не может, но условие α > σ выполняется всегда для любого расхода. Для различных завес, рассмотренных в [1], значение σ соответственно равно 0,07, 0,05, 0,22 и 0,21. Отсюда следует, что малость величины α не является непременным признаком достаточно большого воздушного расхода воздушной завесы, для некоторых завес очень малые значения α принципиально недостижимы.
В работе [1], с которой начинался этот цикл статей, ставился вопрос о характерных воздушных и водяных расходах, определяемых только тепловыми свойствами завес (инвариантами теплопередачи), а не мощностью двигателей крыльчаток и насосов. Если рассмотреть выражение для основного коэффициента мощности теплопередачи С=В/(1+K/(cg)), то его величина определяется безразмерным выражением K/(cg). При малых g коэффициент С достаточно быстро растет в зависимости от расхода воздуха, а при больших g рост замедляется. Итак, искомый характерный воздушный расход g0 = K/c. Что касается характерного водяного расхода, то, к сожалению, выражение D=В/ (1+N/ (cwG)) не может быть использовано для получения выражения для G0, поскольку вследствие отрицательности N оно стремится к бесконечности при уменьшении расхода. Это происходит при очень малых расходах, выходящих за рамки (3). При интересующих же нас умеренных расходах выражение для D является исключительно слабой функцией G. Однако все же можно дать количественную оценку величины этого расхода, если учесть, что в оптимальных областях работы завесы выполняется условие Δ ТW ≈ ΔT. Тогда G0 = K/cw.
Несмотря на то что данная работа и выглядит несколько абстрактной, в ней были даны исчерпывающие ответы на все поставленные в работе [1] вопросы. Хотя рассмотрение воздушных завес при возможности переменного расхода воздуха многократно усложняет предмет исследования по сравнению со случаем фиксированного расхода, именно такое рассмотрение позволяет найти инварианты теплового обмена. Для каждой завесы теперь появляется возможность сравнения ее реального максимального воздушного расхода и некоторого воздушного расхода, характерного для ее тепловых коэффициентов, не зависящих от расхода вообще. Отметим, что все рассмотрения этого цикла касаются не слишком малых расходов воды и воздуха. И если соотношение (21) обычно выполняется для воздушных завес, то расход теплоносителя является по отношению к ним в некотором смысле внешним. А именно — возможны значения расходов теплоносителя, выходящие за границы соотношения (3), которые находятся за пределами оптимальных областей использования воздушных завес. Исследованию таких случаев посвящена работа [5], где для фиксированного достаточно большого воздушного расхода приводится рассмотрение соотношений тепловой мощности завесы для более низких расходов теплоносителя, чем те, которые определяются (3).
В заключительной работе этого цикла статей, которая будет представлена читателям в одном из следующих номеров журнала «МИР КЛИМАТА», все предыдущие соотношения будут переведены в практическую плоскость. Также будут даны рекомендации для производителей и потребителей воздушных завес, касающиеся оптимальных условий использования воздушных завес. Так как эти условия подразумевают достаточно большой расход теплоносителя, в некоторых случаях для расчета практических задач может быть использован однопараметрический или «упрощенный» подход, который был разработан Сергеем Анатольевичем Лысцевым. С основными соотношениями этого подхода можно также ознакомиться в [5]. В заключительной работе цикла будет также представлено обобщение однопараметрического подхода для случая произвольных расходов воздуха.
Автор выражает большую признательность старшему научному сотруднику Национального исследовательского центра «Курчатовский институт» Игорю Игоревичу Николаеву за плодотворное обсуждение математической части работы и ценные замечания, которые привели к ее существенному упрощению.
Литература:
1. Пухов А. В. Мощность тепловой завесы при произвольных расходах теплоносителя и воздуха. Интерпретация опытных данных. «МИР КЛИМАТА» № 80, Москва, 2013.
2. Кейс В. М. Лондон А. Л. Компактные теплообменники, Москва, Энергия, 1967.
3. Уонг Х. Основные формулы и данные по теплообмену для инженеров. Москва, «Атомиздат», 1979.
5. Лысцев С. А. Принципы и подходы к расчету тепловых параметров воздушных завес. «МИР КЛИМАТА» № 83, Москва, 2014.
Алексей Пухов, компания «ТРОПИК»
